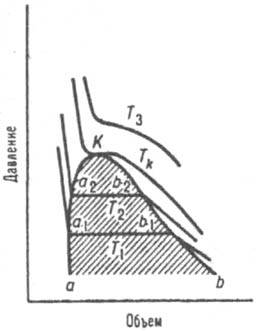
Рис. 1. Диаграмма равновесия жидкость пар для чистого в-ва. Т 1. Т 2, T к, Т 3 - изотермы, К грипп, точка, аКb - пограничная кривая; заштрихована область двухфазного равновесия.
В двойных системах К. с. всегда заканчивается равновесное сосуществование жидкой и паровой фаз, как и в чистых в-вах. Для нск-рых систем с ограниченной взаимной р-римостью компонентов существуют, кроме того, К. с. как предельные случаи равновесного сосуществования двух жидких, двух газовых или двух кристаллич. фаз (твердых р-ров). В нск-рых случаях возможное в принципе К. с. может не реализоваться, если на рассматриваемое двухфазное равновесие накладывается равновесие др. фаз (напр., при понижении т-ры или повышении давления начнется кристаллизация одной или обеих жидких фаз). На диаграмме состояния двойной системы К. с. отвечает критич. кривая. Для любого типа двухфазного равновесия К. с. может быть изображено точкой на диаграмме в координатах хим. потенциал i-го компонента mi - молярная доля этого компонента xi (рис. 2). Ур-ния К. с. имеют вид:
(дmi/дх i)Pк. Тк=0, ( д 2mi/дxi2) Рк. Тк=0.
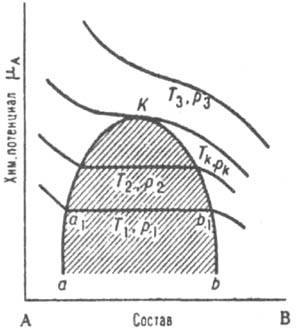
Рис. 2. Зависимость хим. потенциала m А компонента А двойной системы А-В от состава. T1p1,T2p2, T кp к,T3p3 - изотермы-изобары, К - критич. точка, аКb - пограничная кривая; заштрихована область двухфазного равновесия, в к-рой хим. потенциал не зависит от состава.
Согласно этим ур-ниям, в К. с. компонента mi не изменяется при изобарно-изотсрмич. изменении состава системы. Слабая зависимость mi от состава может сохраняться в значит. температурном диапазоне вдали от Т к. Равновесие жидкость - газ на плоской диаграмме состояния в координатах давление - состав изображается изотермами (рис. 3), к-рые состоят из кривых конденсации (сплошные
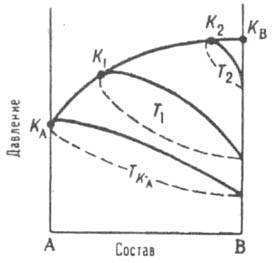
Рис. 3. Диаграмма равновесия жидкость газ для двойной системы А - В. Т KA, Т 1, Т 2 изотермы, К A К 1K2KB, критич. кривая. K А и К B критич, точки чистых А и В соответственно.
линии) и кривых кипения (пунктир). Эти кривые замыкаются в критич. точках К 1, К 2,..., геом. место к-рых К А К 1 К 2 К В является проекцией пространств. критич. кривой в данной системе координат. Критич. кривая заканчивается в критич. точках чистых компонентов К А и К B соответственно. По мере повышения т-ры область двухфазного состояния системы уменьшается, стягиваясь при Т к в точку, совпадающую с критич. точкой более летучего компонента, напр. К B.

Рис. 4. Диаграмма равновесия жидкость - жидкость для двойной системы А - В. К B и KA верхняя и нижняя критич. точки смешения (р-римости) соотв., аК BbК A- пограничная кривая; заштрихована область двухфазного равновесия.
Равновесие жидкость - жидкость может заканчиваться верхней критич. точкой смешения (р-римости) или ниж. критич. точкой смешения (р-римости), в зависимости от того, увеличивается или уменьшается взаимная р-римость компонентов с повышением т-ры. В общем случае система может иметь обе критич. точки; пограничная кривая, отделяющая область гомогенного состояния системы при любых составах от области ее расслаивания на две жидкие фазы, имеет вид замкнутого овала (рис. 4). В двойных системах с ограниченной взаимной р-римостью газов наблюдается К. с. для равновесия газ-газ. Экспериментально обнаружены только ниж. критич. точки смешения газов, хотя в принципе возможно существование и верх. точек. К. с. газов бывает двух типов. Первый обнаружен в смесях, одним из компонентов к-рых является Не. Расслаивание газовой смеси начинается в критич. точке менее
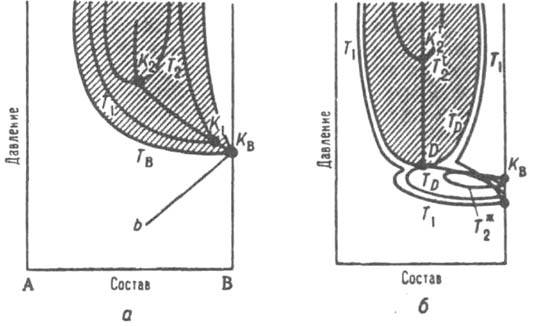
Рис. 5. Диаграмма равновесия газ газ для двойной системы А В. KB, критич точка менее летучего компонента В; заштрихована область двухфазного равновесия газ-газ. а- равновесие газ-газ первого типа; TB Т 1. Т 2 - изотермы равновесия газ газ. К BK1K2 критич. кривая равновесия газ газ, bК B - участок критич. кривой равновесия жидкость - газ; 6 равновесие второго типа: T1, Т D, Т* - изотермы равновесия жидкость газ. TD, Т n2 - изотермы равновесия газ - газ. DK2 - участок критич. кривая равновесия газ-газ, D - двойная критич. точка.
летучего компонента (К B на рис. 5,а). По мере повышения т-ры (изотермы T1, T2,...) интервал составов, соответствующих двухфазному состоянию газовой смеси, сужается, а давление повышается. Вся критич. кривая расположена при более высоких давлениях и т-рах, чем кривые равновесия жидкость - пар. В случае К. с. второго типа расслаивание газовой смеси начинается при т-рe, для к-рой еще наблюдается равновесие жидкость - пар, т. е. при т-ре ниже критич. точки менее летучего компонента К B (рис. 5,5). Изотерма равновесия жидкость-газ соприкасается с изотермой равновесия газ-газ в точке D, к-рая является двойной критич. точкой. Для равновесия кристалл-кристалл К. с. было обнаружено в случае системы палладий - водород (твердый р-р внедрения). Критич. параметры - 19,9 атм и 295,3 oC; ниже этих значений существуют две кристаллич. фазы с одинаковой решеткой, но разл. содержанием водорода, выше - система является гомогенной. Впоследствии было найдено К. с. и для твердых р-ров замещения, напр. в системе NaCl-KCl. Критич. кривые могут иметь особые точки, в к-рых термодинамич. поведение системы отличается от поведения в остальных точках критич. кривой. Особыми точками являются, напр., критич. точки равновесия жидкость-пар в случае бесконечно разбавленных р-ров. Их особенность состоит в том, что в пределах xi:0 значения нек-рых св-в системы зависят от пути подхода к этому пределу. Напр., парциальный молярный объем р-рителя равен молярному объему чистого р-рителя только в том случае, если переход х i:0 происходит при давлениях и т-рах, к-рые являются критич. параметрами для чистого р-рителя, вдали от критич. точки парциальный молярный объем р-рителя в бесконечно разбавленном р-ре при любых т-рах и давлениях равен молярному объему чистого р-рителя. Критич. точка азеотропной смеси, а также точки минимума или максимума на критич. кривой тоже считаются особыми. Для системы, показанной на рис. 5, б. особой точкой считается точка D, т. к. в ней кривые зависимости составов равновесных жидкости и пара от давления изменяют направление на противоположное. В многокомпонентных системах также возможны двухфазные равновесия разл. типов, оканчивающиеся К. с. В тройных системах критич. точки образуют критич. пов-сть с несколькими особыми точками. наиб. важно появление критич. точек высшего порядка, в к-рых сливаются критич. кривые равновесий жидкость - жидкость (в присут. газовой фазы) и жидкость-пар (в присут. второй жидкой фазы).
Осн. положения классич. (феноменологич.) теории К. с. были сформулированы Дж. .Гиббсом и обобщены Л. Д. Ландау. Эта теория позволяет предсказать поведение в-ва в К. с. по известным св-вам двухфазного состояния. Расчеты по совр. флуктуац. теории дают более точное соответствие опытным данным. Изучение К. с. имеет важное практич. значение. Мн. технол. процессы, в частности нефте- и газодобывающие, высокотемпературные энергетические, протекают в условиях, близких к критич. параметрам систем, и в закритич. области параметров. Для разработки и проектирования таких процессов важно знать общую картину фазовых равновесий, включая все их границы (критич. кривые), а также особенности поведения систем вблизи К. с. и в закритич. области. Лит.: Фишер М.. Природа критического состояния, пер. с англ.. М.. 1968; ЦиклисД. С, Расслоение газовых смесей, М.. 1969; Кричевский И. Р., Термодинамика критических бесконечно разбавленных растворов. М.. 1975: Xазанова H. E.. Системы с азеотропизмом при высоких давлениях. М.. 1978. См. также лиг. при сг. Критические явления. Н. E. Хазанова.
Химическая энциклопедия. — М.: Советская энциклопедия. Под ред. И. Л. Кнунянца. 1988.