(от лат. orbita-путь, колея), волновая ф-ция, описывающая состояние одного электрона в атоме, молекуле или др. квантовой системе. В общем случае квантовохим. термин "О." используется для любой ф-ции 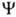 , зависящей от переменных х, у, z одного электрона. В рамках молекулярных орбиталей методов для электронных состояний молекул часто используют приближенное описание квантовой системы как целого, задавая состояние электрона в усредненном поле, созданном ядрами и остальными электронами системы. При этом О.
, зависящей от переменных х, у, z одного электрона. В рамках молекулярных орбиталей методов для электронных состояний молекул часто используют приближенное описание квантовой системы как целого, задавая состояние электрона в усредненном поле, созданном ядрами и остальными электронами системы. При этом О.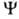 определяется одноэлектронным ур-ни-ем Шрёдингера с эффективным одноэлектронным гамильтонианом
определяется одноэлектронным ур-ни-ем Шрёдингера с эффективным одноэлектронным гамильтонианом 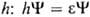 ; орбитальная энергия
; орбитальная энергия 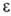 , как правило, соотносится с потенциалом ионизации (см. Купманса теорема). В зависимости от системы, для к-рой определена О., различают атомные, молекулярные и кристаллические О.
, как правило, соотносится с потенциалом ионизации (см. Купманса теорема). В зависимости от системы, для к-рой определена О., различают атомные, молекулярные и кристаллические О.
Атомные О. (АО) характеризуются тремя квантовыми числами: главным п, орбитальным / и магнитным ш. Значение l = 0, 1, 2,... задает квадрат орбитального (углового) момента электрона 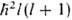 (
(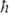 -постоянная Планка), значение m = l,l Ч 1,..., +1, 0, Ч 1,..., Ч l + 1, Ч l-проекцию момента на нек-рую выбранную ось z; n нумерует орбитальные энергии. Состояния с заданным / нумеруются числами п= l + 1, l + 2,... В сферич. системе координат с центром на ядре атома АО имеет форму
-постоянная Планка), значение m = l,l Ч 1,..., +1, 0, Ч 1,..., Ч l + 1, Ч l-проекцию момента на нек-рую выбранную ось z; n нумерует орбитальные энергии. Состояния с заданным / нумеруются числами п= l + 1, l + 2,... В сферич. системе координат с центром на ядре атома АО имеет форму 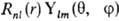 , где
, где 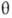 и
и 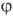 -полярные углы, r-расстояние от электрона до ядра.
-полярные углы, r-расстояние от электрона до ядра. 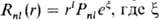 - показатель орбитальной экспоненты, а Р пl-> полином степени ( п Ч l Ч1). В сокращенной записи АО описывают символом
- показатель орбитальной экспоненты, а Р пl-> полином степени ( п Ч l Ч1). В сокращенной записи АО описывают символом
Более удобны АО, содержащие не комплексные сферич. гармоники, а их линейные комбинации, имеющие веществ. значения. Такие АО наз. кубическими (тессераль-ными). Они имеют вид 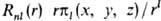 , где
, где 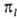 ( х, y, z) - однородный полином (угловая ф-ция) степени l относительно декартовых координат электрона х, у, z с центром на ядре (направление осей произвольно); АО обозначают символами
( х, y, z) - однородный полином (угловая ф-ция) степени l относительно декартовых координат электрона х, у, z с центром на ядре (направление осей произвольно); АО обозначают символами 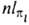 , напр.
, напр.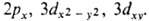
Если полином
nl(r> )определяется решением ур-ния Шрёдингера для электрона в кулоновском поле ядра, АО наз. водородоподобными. Наиб. употребительные водоро-доподобные кубич. АО приведены в таблице.
ВОДОРОДОПОДОБНЫЕ ОРБИТАЛИ s. p, d, f -ТИПОВ
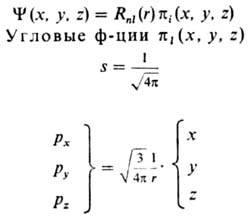

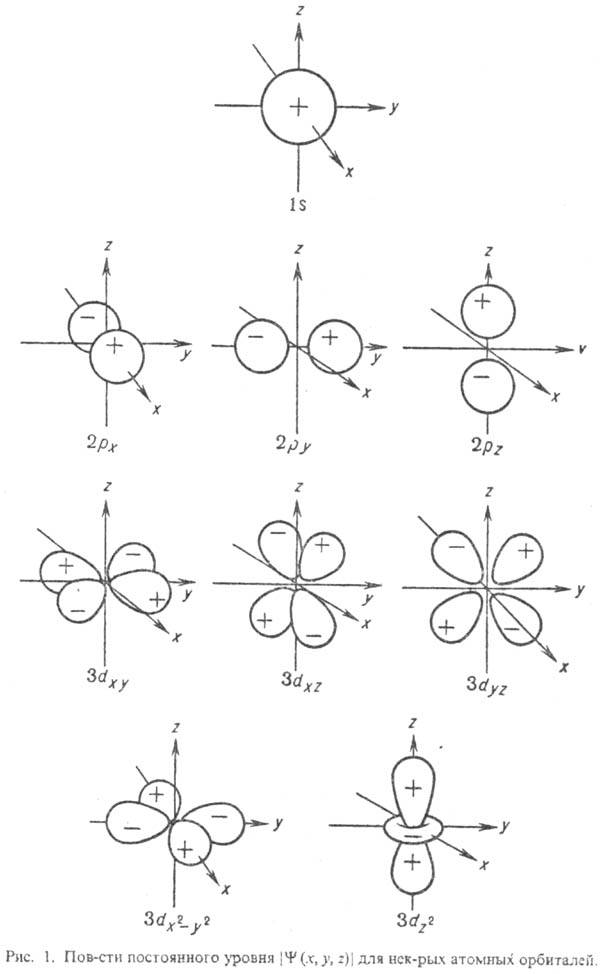
В хим. приложениях нередко приводят контуры АО, к-рые м. б. построены по-разному. Наиб. распространены т. наз. фазовые пов-сти, на к-рых изображают значения кубич. (или сферич.) гармоник: при заданных полярных углах модуль угловой части АО равен расстоянию до начала координат. На рис. 1 приведены другие, более наглядные пов-сти, на к-рых абс. величины нек-рых АО имеют постоянное значение. Оба способа изображения АО практически не различаются лишь вблизи начала координат. Во всех случаях знаками + и Ч (или штриховкой) указывают, какой знак имеет АО в данной области. Как и все волновые ф-ции, АО можно умножить на Ч 1, что приведет к изменению знака ф-ции, однако смысл имеют не знаки АО сами по себе, а чередование знаков для системы АО при описании мол. орбиталей. Графич. изображение АО не всегда имеет смысл. Так, квадраты модулей сферич. гармоник не зависят от угла  , поэтому изображение, напр., АО 2р х и 2р у будет совсем не похоже на изображение АО 2 р + и 2
, поэтому изображение, напр., АО 2р х и 2р у будет совсем не похоже на изображение АО 2 р + и 2
-, хотя обе пары АО полностью эквивалентны.
Молекулярные О. (МО) описывают электрон в поле всех ядер молекулы и усредненном поле остальных электронов. Как правило, МО не имеют простого аналит. представления и для них используют приближение линейной комбинации атомных орбиталей (см. ЛКАО-приближение). В методах мол. орбиталей многоэлектронная волновая ф-ция строится как произведение или определитель, составленный из спин-орбиталей, т. е. О., умноженных на спин-функцию  или
или  (см. Паули принцип).
(см. Паули принцип).
Для молекул с симметричной ядерной конфигурацией МО классифицируют по типам симметрии. Напр., МО любой молекулы с аксиальной симметрией, в т. ч. двухатомной молекулы, можно классифицировать по поведению относительно поворотов вокруг оси молекулы (как правило, оси z). Если  -набор координат электрона, напр. цилиндрических, в к-ром выделен угол
-набор координат электрона, напр. цилиндрических, в к-ром выделен угол 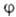 поворота вокруг оси, все МО можно представить в форме
поворота вокруг оси, все МО можно представить в форме 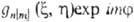 , где т =0, b 1, b2, b3,..., а пнумерует орбитальные энергии ( п =1, 2, 3...). При т Ч0 такая О. не меняется при поворотах и наз. s-орбиталью. При m
, где т =0, b 1, b2, b3,..., а пнумерует орбитальные энергии ( п =1, 2, 3...). При т Ч0 такая О. не меняется при поворотах и наз. s-орбиталью. При m 0 уровни с одинаковыми значениями
0 уровни с одинаковыми значениями 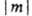 двукратно вырождены. По аналогии с АО принято обозначать МО символами
двукратно вырождены. По аналогии с АО принято обозначать МО символами 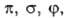 ..., если они отвечают
..., если они отвечают 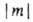 = 1, 2, 3... Аксиальносимметричные МО обозначают символами
= 1, 2, 3... Аксиальносимметричные МО обозначают символами 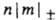 (справа внизу указывают знак т), напр. 2
(справа внизу указывают знак т), напр. 2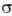 ,1
,1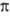 +, 2
+, 2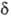 -. Как и в случае атомов, нередко используются вещественнозначные формы МО, в к-рых зависимость от j описывается простыми ф-циями декартовых координат. Соответственно возникают МО типа
-. Как и в случае атомов, нередко используются вещественнозначные формы МО, в к-рых зависимость от j описывается простыми ф-циями декартовых координат. Соответственно возникают МО типа 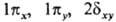 и т. д. Гомоядерная молекула имеет дополнительно центр инверсии; МО, не меняющие при инверсии знак, наз. ч е т н ы м и, а меняющие-нечетными; четность МО указывается ниж. индексами g (четная) или и(нечетная).
и т. д. Гомоядерная молекула имеет дополнительно центр инверсии; МО, не меняющие при инверсии знак, наз. ч е т н ы м и, а меняющие-нечетными; четность МО указывается ниж. индексами g (четная) или и(нечетная).
В многоатомной молекуле симметричность ядерной конфигурации отражается в том, что при повороте вокруг главной оси симметрии орбитали либо не меняются (МО типа а),либо меняют знак (МО типа b) Симметричность или антисимметричность относительно отражения в плоскости, содержащей главную ось, либо относительно поворота вокруг оси 2-го порядка, перпендикулярной главной оси симметрии, указывают ниж. индексами 1 или 2 соотв., а в случае плоскости, перпендикулярной оси,-одним или двумя штрихами. Симметрия относительно инверсии указывается ниж. индексами ди и, как и для двухатомных молекул. Напр., в молекуле с симметрией D4h орбиталь 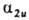 симметрична относительно поворота вокруг главной оси 4-го порядка, антисимметрична относительно поворота вокруг перпендикулярной оси 2-го порядка и относительно инверсии. Если при поворотах МО переходит в комбинацию двух (или трех) МО, как это имеет место для МО типа
симметрична относительно поворота вокруг главной оси 4-го порядка, антисимметрична относительно поворота вокруг перпендикулярной оси 2-го порядка и относительно инверсии. Если при поворотах МО переходит в комбинацию двух (или трех) МО, как это имеет место для МО типа 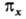 и
и 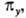 она обозначается символом "e" (или f) с соответствующими индексами (употребителен также символ t).
она обозначается символом "e" (или f) с соответствующими индексами (употребителен также символ t).
Изменение знака МО при отражении в плоскости означает, что в этой плоскости МО обращается в нуль. С ростом числа узловых плоскостей МО, вообще говоря, отвечает все более высоким значениям орбитальных энергий.
Для систем, где имеются локальные плоскости симметрии, напр. для молекул с ненасыщ. связями, МО обозначают не так, как следовало бы для группы симметрии С g т. е. не a' или а:, а используют обозначения, аналогичные обозначениям МО двухатомных молекул: МО, симметричные относительно плоскости, обозначаются как 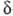 -орбитали, а антисимметричные относительно плоскости - как
-орбитали, а антисимметричные относительно плоскости - как 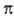 -орбитали. Поскольку
-орбитали. Поскольку 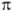 -орбитали заведомо имеют плоскость симметрии, в к-рой они обращаются в нуль, орбитальные энергии МО возрастают в ряду
-орбитали заведомо имеют плоскость симметрии, в к-рой они обращаются в нуль, орбитальные энергии МО возрастают в ряду 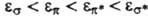 , где * означает разрыхляющую орбиталь (см. ниже). Орбитали, отвечающие неподеленной паре электронов, обозначаются как п.
, где * означает разрыхляющую орбиталь (см. ниже). Орбитали, отвечающие неподеленной паре электронов, обозначаются как п.
Под действием электромагн. поля наиб. вероятны переходы с изменением состояния лишь одного из электронов, поэтому при описании квантовых переходов в сопряженных системах принято указывать лишь символы соответствующих МО; напр., в ненасыщ. системах возможны переходы 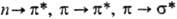 и т. п.
и т. п.
В рамках ЛКАО-приближения МО можно связать с О. атомов, образующих молекулу. Если орбитальная энергия, отвечающая электрону в молекуле, ниже, чем в атоме, МО наз. связывающей, если выше-разрыхляющей. Если же орбитальная энергия при переходе от атомов к молекуле почти не изменяется, как в случае неподеленных пар электронов, МО наз. несвязывающей.
Схематически образование МО из АО часто передают корреляц. диаграммами. Правила построения кор-реляц. диаграмм состоят в том, что наиб, вклад в МО дают АО с близкими орбитальными энергиями. Кроме того, эти АО должны относиться к одному типу симметрии относительно операций симметрии молекулы. Напр., в случае диаграммы, представленной на рис. 2, АО типа 2р х в молекуле оказывается  -орбиталью, а АО типа 2р. -
-орбиталью, а АО типа 2р. - -орби-талью, т. е. АО 2р х и 2р z не должны одновременно входить в состав одной и той же МО.
-орби-талью, т. е. АО 2р х и 2р z не должны одновременно входить в состав одной и той же МО.
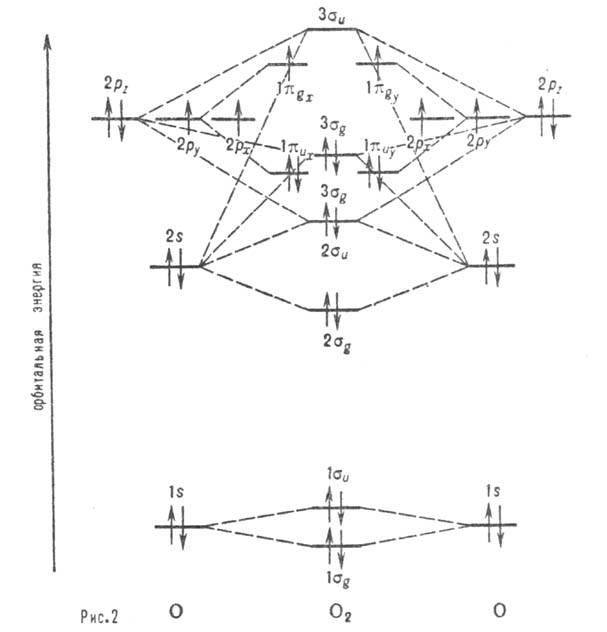
Рис. 2. Корреляц. диаграмма для молекулы О 2. Горизонтальные линии отвечают энергиям атомных и мол. орбиталей. Пунктирные линии указывают, в какие мол. орбитали входят данная атомная орбиталь с большим вкладом. Орбитали  -связывающие, а
-связывающие, а  -разрыхляющие. Стрелками обозначено заполнение орбиталей в основном (низшем по энергии) состояния молекулы О 2 (триплетное состояние).
-разрыхляющие. Стрелками обозначено заполнение орбиталей в основном (низшем по энергии) состояния молекулы О 2 (триплетное состояние).
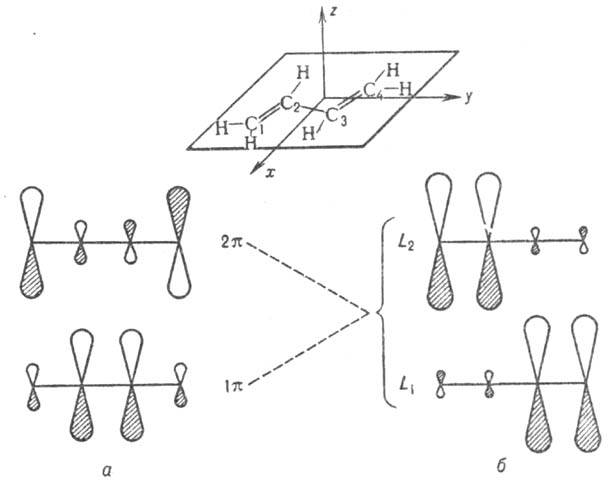
Рис. 3. Занятые p-орбитали основного состояния 1,3-бутадиена; а- 1 - и 2
- и 2 -орбитали; б-локализованные орбитали p-типа, полученные из 1
-орбитали; б-локализованные орбитали p-типа, полученные из 1 - и 2
- и 2 -орбиталей. Орбитали расположены в порядке возрастания орбитальных энергий.
-орбиталей. Орбитали расположены в порядке возрастания орбитальных энергий.
Обычно МО изображают графически, указывая систему АО 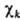 , ее образующих (рис. 3). При этом изображают контуры АО, расположенных вблизи соответствующих ядер молекулы. Размеры АО на рис. отражают величину коэф. перед ней в представлении МО , а знаки (фазы) АО учитывают знак
, ее образующих (рис. 3). При этом изображают контуры АО, расположенных вблизи соответствующих ядер молекулы. Размеры АО на рис. отражают величину коэф. перед ней в представлении МО , а знаки (фазы) АО учитывают знак 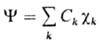 приложениях применяют несимметричные О., локализованные в отдельных областях пространства и описывающие в этих областях распределение электронной плотности. Закономерности строения локализованных О. в эквивалентных фрагментах разл. молекул часто связывают с предоставлением о гибридизации АО.
приложениях применяют несимметричные О., локализованные в отдельных областях пространства и описывающие в этих областях распределение электронной плотности. Закономерности строения локализованных О. в эквивалентных фрагментах разл. молекул часто связывают с предоставлением о гибридизации АО.
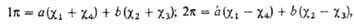
где 0 = 0,372, b = 0,602, 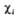 -атомная орбиталь 2pz атома С i (i=1, 2, 3, 4). 1
-атомная орбиталь 2pz атома С i (i=1, 2, 3, 4). 1 -орбиталь имеет одну узловую плоскость ( ху), 2
-орбиталь имеет одну узловую плоскость ( ху), 2 -орбиталь имеет дополнит. узловую плоскость, перпендикулярную этой плоскости и проходящую между атомами С 2 и С 3. Локализованные орбитали отвечают в осн. хим. связям C1 ЧС 2 (L1) и C3-C4 (L2): L1=
-орбиталь имеет дополнит. узловую плоскость, перпендикулярную этой плоскости и проходящую между атомами С 2 и С 3. Локализованные орбитали отвечают в осн. хим. связям C1 ЧС 2 (L1) и C3-C4 (L2): L1=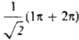 , L2 = . Напр., L1 = с(
, L2 = . Напр., L1 = с( 1 +
1 + 2) + d(
2) + d(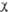 з -
з -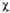 4), где d= 0,162, с= 0,689. Изолир.
4), где d= 0,162, с= 0,689. Изолир. 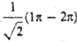 двойной связи С 1=C2 отвечает орбиталь я-типа 0,707
двойной связи С 1=C2 отвечает орбиталь я-типа 0,707
Химическая энциклопедия. — М.: Советская энциклопедия. Под ред. И. Л. Кнунянца. 1988.