раздел математики, дающий методы количественного исследования разных процессов изменения; занимается изучением скорости изменения (дифференциальное исчисление) и определением длин кривых, площадей и объемов фигур, ограниченных кривыми контурами и поверхностями (интегральное исчисление). Для задач математического анализа характерно, что их решение связано с понятием предела. Начало математическому анализу положил в 1665 И. Ньютон и (около 1675) независимо от него Г. Лейбниц, хотя важную подготовительную работу провели И. Кеплер (1571-1630), Ф. Кавальери (1598-1647), П. Ферма (1601-1665), Дж. Валлис (1616-1703) и И. Барроу (1630-1677). Чтобы сделать изложение более живым, мы будем прибегать к языку графиков. Поэтому читателю, возможно, будет полезно заглянуть в статью
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ,
прежде чем приступать к чтению данной статьи.
ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
Касательные. На рис. 1 показан фрагмент кривой y = 2x - x2, заключенный между x = -1 и x = 3. Достаточно малые отрезки этой кривой выглядят прямыми. Иначе говоря, если Р - произвольная точка этой кривой, то существует некоторая прямая, проходящая через эту точку и являющаяся приближением кривой в малой окрестности точки Р, причем чем меньше окрестность, тем лучше приближение. Такая прямая называется касательной к кривой в точке Р. Основная задача дифференциального исчисления заключается в построении общего метода, позволяющего находить направление касательной в любой точке кривой, в которой касательная существует. Нетрудно представить себе кривую с резким изломом (рис. 2). Если Р - вершина такого излома, то можно построить аппроксимирующую прямую PT1 - справа от точки Р и другую аппроксимирующую прямую РТ2 - слева от точки Р. Но не существует единственной прямой, проходящей через точку Р, которая одинаково хорошо приближалась к кривой в окрестности точки P как справа, так и слева, следовательно касательной в точке P не существует.

Рис. 1.

Рис. 2.
На рис. 1 касательная ОТ проведена через начало координат О = (0,0). Угловой коэффициент этой прямой равен 2, т.е. при изменении абсциссы на 1 ордината увеличивается на 2. Если x и y - координаты произвольной точки на ОТ, то, удаляясь от О на расстояние х единиц вправо, мы удаляемся от О на 2y единиц вверх. Следовательно, y/x = 2, или y = 2x. Это уравнение касательной ОТ к кривой y = 2x - x2 в точке О. Необходимо теперь объяснить, почему из множества прямых, проходящих через точку О, выбрана именно прямая ОТ. Чем же прямая с угловым коэффициентом 2 отличается от других прямых? Существует один простой ответ, и нам трудно удержаться от искушения привести его, используя аналогию с касательной к окружности: касательная ОТ имеет с кривой только одну общую точку, тогда как любая другая невертикальная прямая, проходящая через точку О, пересекает кривую дважды. В этом можно убедиться следующим образом. Поскольку выражение y = 2x - x2 можно получить вычитанием х2 из y = 2x (уравнения прямой ОТ), то значения y для графика оказываются меньше знаний y для прямой во всех точках, за исключением точки x = 0. Следовательно, график всюду, кроме точки О, расположен ниже ОТ, и эта прямая и график имеют только одну общую точку. Кроме того, если y = mx - уравнение какой-нибудь другой прямой, проходящей через точку О, то обязательно найдутся две точки пересечения. Действительно, mx = 2x - x2 не только при x = 0, но и при x = 2 - m. И только при m = 2 обе точки пересечения совпадают. На рис. 3 показан случай, когда m меньше 2, поэтому справа от О возникает вторая точка пересечения.

Рис. 3.
То, что ОТ - единственная невертикальная прямая, проходящая через точку О и имеющая с графиком лишь одну общую точку, не самое главное ее свойство. Действительно, если мы обратимся к другим графикам, то вскоре выяснится, что отмеченное нами свойство касательной в общем случае не выполняется. Например, из рис. 4 видно, что вблизи точки (1,1) график кривой y = x3 хорошо аппроксимируется прямой РТ, имеющей однако, с ним более одной общей точки. Тем не менее, нам хотелось бы считать РТ касательной к этому графику в точке Р. Поэтому необходимо найти какой-то иной способ выделения касательной, чем тот, который так хорошо послужил нам в первом примере.

Рис. 4.
Предположим, что через точку О и произвольную точку Q = (h,k) на графике кривой y = 2x - x2 (рис. 5) проведена прямая (называемая секущей). Подставляя в уравнение кривой значения x = h и y = k, получаем, что k = 2h - h2, следовательно, угловой коэффициент секущей равен
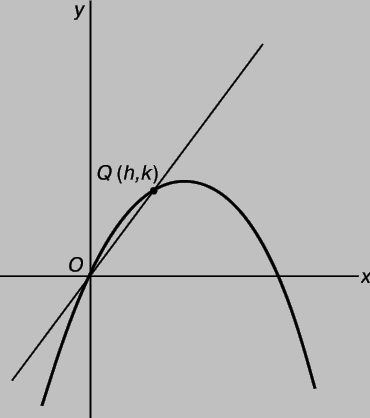
Рис. 5.

При очень малых h значение m близко к 2. Более того, выбирая h достаточно близким к 0, мы можем сделать m сколь угодно близким к 2. Можно сказать, что m "стремится к пределу", равному 2, когда h стремится к нулю, или что предел m равен 2 при h, стремящемся к нулю. Символически это записывается так:

Тогда касательная к графику в точке О определяется как прямая, проходящая через точку О, с угловым коэффициентом, равным этому пределу. Такое определение касательной применимо в общем случае. Покажем преимущества этого подхода еще на одном примере: найдем угловой коэффициент касательной к графику кривой y = 2x - x2 в произвольной точке P = (x,y), не ограничиваясь простейшим случаем, когда P = (0,0). Пусть Q = (x + h, y + k) - вторая точка на графике, находящаяся на расстоянии h справа от Р (рис. 6). Требуется найти угловой коэффициент k/h секущей PQ. Точка Q находится на расстоянии


Рис. 6.
над осью х. Раскрывая скобки, находим:

Вычитая из этого уравнения y = 2x - x2, находим расстояние по вертикали от точки Р до точки Q:

Следовательно, угловой коэффициент m секущей PQ равен

Теперь, когда h стремится к нулю, m стремится к 2 - 2x; последнюю величину мы и примем за угловой коэффициент касательной PT. (Тот же результат получится, если h принимает отрицательные значения, что соответствует выбору точки Q слева от P.) Заметим, что при x = 0 полученный результат совпадает с предыдущим. Выражение 2 - 2x называется производной от 2x - x2. В старину производную также называли "дифференциальным отношением" и "дифференциальным коэффициентом". Если выражением 2x - x2 обозначить f(x), т.е.

то производную можно обозначить

Для того, чтобы узнать угловой коэффициент касательной к графику функции y = f(x) в какой-нибудь точке, необходимо подставить в f'(x) соответствующее этой точке значение х. Таким образом, угловой коэффициент f'(0) = 2 при х = 0, f'(0) = 0 при х = 1 и f'(2) = -2 при х = 2. Производную также обозначают у', dy/dx, Dхy и Dу. Тот факт, что кривая y = 2x - x2 вблизи данной точки практически неотличима от ее касательной в этой точке, позволяет говорить об угловом коэффициенте касательной как об "угловом коэффициенте кривой" в точке касания. Такие образом, мы можем утверждать, что угловой коэффициент рассматриваемой нами кривой имеет в точке (0,0) угловой коэффициент 2. Можно также сказать, что при x = 0 скорость изменения y относительно x равна 2. В точке (2,0) угловой коэффициент касательной (и кривой) равен -2. (Знак минус означает, что при возрастании x переменная y убывает.) В точке (1,1) касательная горизонтальна. Мы говорим, что кривая y = 2x - x2 имеет в этой точке стационарное значение.
Максимумы и минимумы. Мы только что показали, что кривая f(x) = 2x - x2 стационарна в точке (1,1). Так как f'(x) = 2 - 2x = 2(1 - x), ясно, что при x, меньших 1, f'(x) положительна, и, следовательно, y возрастает; при x, больших 1, f'(x) отрицательна, и поэтому y убывает. Таким образом, в окрестности точки (1,1), обозначенной на рис. 6 буквой М, значение у растет до точки М, стационарно в точке М и убывает после точки М. Такая точка называется "максимумом", поскольку значение у в этой точке превосходит любые его значения в достаточно малой ее окрестности. Аналогично, "минимум" определяется как точка, в окрестности которой все значения y превосходят значение у в самой этой точке. Может также случиться, что хотя производная от f (x) в некоторой точке и обращается в нуль, ее знак в окрестности этой точки не меняется. Такая точка, не являющаяся ни максимумом, ни минимумом, называется точкой перегиба. В качестве примера найдем стационарную точку кривой

Производная этой функции равна

и обращается в нуль при x = 0, х = 1 и х = -1; т.е. в точках (0,0), (1, -2/15) и (-1, 2/15). Если х чуть меньше -1, то f'(x) отрицательна; если х чуть больше -1, то f'(x) положительна. Следовательно, точка (-1, 2/15) - максимум. Аналогично, можно показать, что точка (1, -2/15) - минимум. Но производная f'(x) отрицательна как до точки (0,0), так и после нее. Следовательно, (0,0) - точка перегиба. Проведенное исследование формы кривой, а также то обстоятельство, что кривая пересекает ось х при f(x) = 0 (т.е. при х = 0 или

) позволяют представить ее график примерно так, как показано на рис. 7.

Рис. 7.
В общем, если исключить необычные случаи (кривые, содержащие прямолинейные отрезки или бесконечное число изгибов), существуют четыре варианта взаимного расположения кривой и касательной в окрестности точки касания Р. (См. рис. 8, на котором касательная имеет положительный угловой коэффициент.) 1) По обе стороны от точки Р кривая лежит выше касательной (рис. 8,а). В этом случае говорят, что кривая в точке Р выпукла вниз или вогнута.
2) По обе стороны от точки Р кривая расположена ниже касательной (рис. 8,б). В этом случае говорят, что кривая выпукла вверх или просто выпукла. 3) и 4) Кривая располагается выше касательной по одну сторону от точки Р и ниже - по другую. В этом случае Р - точка перегиба. Сравнивая значения f'(x) по обе стороны от Р с ее значением в точке Р, можно определить, с каким из этих четырех случаев приходится иметь дело в конкретной задаче.
Приложения. Все изложенное выше находит важные приложения в различных областях. Например, если тело брошено вертикально вверх с начальной скоростью 200 футов в секунду, то высота s, на которой они будут находиться через t секунд по сравнению с начальной точкой составит

Действуя так же, как в рассмотренных нами примерах, находим

эта величина обращается в нуль при

, затем становится стационарной, а после убывает. Таково общее описание движения брошенного вверх тела. Из него мы узнаем, когда тело достигает высшей точки. Далее, подставляя t = 25/4 в f (t), мы получаем 625 футов, максимальную высоту подъема. В данной задаче f'(t) имеет физический смысл. Эта производная показывает скорость, с которой тело движется в момент времени t. Рассмотрим теперь приложение другого типа (рис. 9). Из листа картона площадью 75 см2 требуется изготовить коробку с квадратным дном. Каковы должны быть размеры этой коробки, чтобы она имела максимальный объем? Если х - сторона основания коробки и h - ее высота, то объем коробки равен V = x2h, а площадь поверхности равна 75 = x2 + 4xh. Преобразуя уравнение, получаем:>">
с и отрицательна по истечении этого времени. Следовательно, s возрастает до

, затем становится стационарной, а после убывает. Таково общее описание движения брошенного вверх тела. Из него мы узнаем, когда тело достигает высшей точки. Далее, подставляя t = 25/4 в f (t), мы получаем 625 футов, максимальную высоту подъема. В данной задаче f'(t) имеет физический смысл. Эта производная показывает скорость, с которой тело движется в момент времени t. Рассмотрим теперь приложение другого типа (рис. 9). Из листа картона площадью 75 см2 требуется изготовить коробку с квадратным дном. Каковы должны быть размеры этой коробки, чтобы она имела максимальный объем? Если х - сторона основания коробки и h - ее высота, то объем коробки равен V = x2h, а площадь поверхности равна 75 = x2 + 4xh. Преобразуя уравнение, получаем:">
