Геометрия - раздел математики, тесно связанный с понятием пространства; в зависимости от форм описания этого понятия возникают различные виды геометрии. Предполагается, что читатель, приступая к чтению этой статьи, обладает некоторыми представлениями об элементарной геометрии, а также о законах арифметики и алгебры.
См. также
АЛГЕБРА;
АРИФМЕТИКА;
ГЕОМЕТРИЯ.
Первый важный вопрос: как описать наше понятие пространства? В поисках ответа перед нами открывается несколько возможностей, но проще, а возможно, естественнее и полезнее воспользоваться для этого понятиями "точка" и "прямая". Оба они коренятся в процессе визуального восприятия. Точку можно мысленно представлять как "точку зрения", из которой ведется наблюдение, а прямую, определяемую двумя объектами, считать состоящей из множества точек зрения, при наблюдении из которых один объект заслоняет другой. При таком подходе вводится понятие "прямизны", которое воплощается в термине "прямая линия" (или просто "прямая"). Можно считать, что мы абстрагировали понятия "точка" и "прямая" из окружающего мира. В нашем повседневном опыте коренится еще одно представление - о расстоянии АВ между точками А и В. (Мы говорим также о "длине" отрезка АВ.) О расстоянии мы судим, сравнивая его с некоторым эталоном. Одна из возможных единиц длины - метр; изготовив копии с эталона метра, мы сравниваем расстояния и говорим, что расстояние АВ больше (>), равно (=) или меньше () некоторого другого расстояния CD. Выбрав какую-либо прямую АВ и точку С, не лежащую на этой прямой, мы можем мысленно представить себе совокупность всех прямых, проходящих через точку С и различные точки прямой АВ. Все эти прямые лежат в плоскости АВС, определяемой точками А, В, С. Это обстоятельство вынуждает нас рассматривать понятие расстояния в более широком контексте; в частности, на плоскости АВС нас могут интересовать точки Р, находящиеся на постоянном расстоянии r от точки С. Тут уместно ввести понятие вращения вокруг точки С и сказать, что все такие точки лежат на "окружности" радиуса r с центром в точке С. Физически мы можем представить себе веревку длиной r, один конец которой закреплен в точке С; туго натянув веревку и вращая ее вокруг точки С, мы опишем другим концом окружность радиуса r, лежащую в плоскости АВС. Из нашего опыта мы знаем, что если радиус достаточно велик, то окружность пересечет прямую АВ в двух точках Р1 и Р2. Если мы начнем поворачивать отрезки Р1С и Р2С вокруг точек Р1 и Р2, то, как известно, найдется такая точка Сў, что P1C = P1Cў и P2C = P2Cў; будем говорить, что прямая ССў "перпендикулярна" прямой АВ (рис. 1). Нет сомнения в том, что ССў пересечет АВ в некоторой точке D; все углы между АВ и CD мы назовем "прямыми углами", а длину d перпендикулярна CD - "расстоянием" от точки С до прямой АВ. Таким образом, мы получим практический способ построения перпендикуляра, "опущенного" из точки С на прямую АВ, и деления отрезка пополам (P1D = DP2).
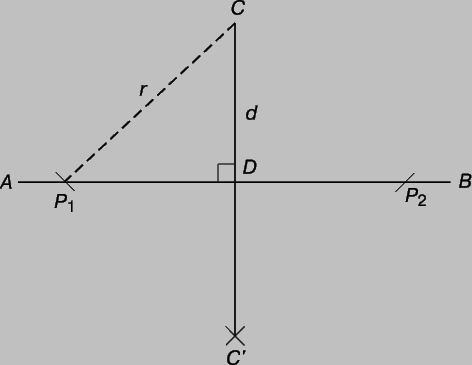
Рис. 1. ТЕОРЕМА ПИФАГОРА утверждает, что квадрат гипотенузы равен сумме квадратов катетов: (P1C)2 = (P1D)2 + (DC)2.
Греческая геометрия. Все эти исследования геометрических отношений в окружающем их мире были сделаны обитателями древних цивилизаций до 4 в. до н.э., когда Евклид свел накопленные к тому времени математические знания в стройную логическую систему. Сейчас практически невозможно сказать, кому принадлежит та или иная теорема в Началах Евклида или кто сделал первый шаг по пути математического открытия. Однако есть исключения. Здесь имеется в виду прежде всего имя Пифагора, который в 6 в. до н.э. заметил, что площадь квадрата, построенного на гипотенузе прямоугольного треугольника, равна сумме площадей, построенных на его катетах. На рис. 1 (P1C)2 = (P1D)2 + (DC)2. Отсюда следует, что квадрат гипотенузы равен сумме квадратов катетов. Начала Евклида начинаются с определений и аксиом, затем идут пять постулатов, из которых первые четыре утверждают: между любыми двумя точками можно провести прямую; любую прямую можно продолжить бесконечно; из всякого центра любым радиусом можно описать окружность; все прямые углы равны между собой. Ретроспективно постичь эти идеи не так уж трудно. Однако осознать их в качестве свойств нашего понятия пространства и абстрагировать таким образом, чтобы их можно было организовать в непротиворечивую систему, непросто; это явилось в свое время одним из величайших достижений человечества. Изложение Евклида было не лишено недостатков, о которых у нас пойдет речь ниже, но дерзость, с которой он осуществил свой замысел, не может не восхищать. В частности, столкнувшись с проблемой определения природы геометрического места точек плоскости р, находящихся на заданном расстоянии d от прямой l, лежащей в плоскости р, Евклид принял формальное предположение - пятый постулат (постулат о параллельных). Согласно этому постулату, если точка Р, принадлежащая плоскости р, не лежит на прямой l, лежащей в плоскости р, то существует только одна прямая lў в р, проходящая через точку Р, такая, что каждая точка прямой lў находится на одном и том же расстоянии d от прямой l; говорят, что lў "параллельна" l (рис. 2). Пятый постулат расходится с наблюдениями внешнего мира: обычно нам кажется, что параллельные прямые (например, железнодорожные рельсы) сходятся на горизонте. К этому вопросу мы в дальнейшем еще вернемся.
Начала Евклида состояли из 13 книг, в которых систематически изложены математические знания его времени относительно пространственных понятий, включая геометрическое представление рациональных чисел. Среди тех, кто жил и творил после Евклида, выделяется прежде всего Архимед (ок. 287-212 до н.э.), чьи взгляды на мир были гораздо шире. Для него непременным атрибутом внешнего мира является движение и все, что с ним связано. Архимед заложил основы механики как науки, а также предвосхитил методы интегрального исчисления, которые впоследствии вошли в т.н. математический анализ. Именно Архимеду принадлежит заслуга осознания весьма любопытного факта, составляющего неотъемлемую часть нашего понимания пространства. Мы предполагаем, что можем достичь любой точки на прямой, сделав достаточное число шагов одной и той же длины. Это кажущееся очевидным допущение, ныне известное как аксиома Архимеда, играет важную роль в основаниях геометрии. Ранее в этой связи философ Зенон в 5 в. до н.э. поднял ряд трудных вопросов об истолковании понятий "точка" и "прямая", ставших головной болью философов и математиков вплоть до 19 в. Одна из знаменитых "апорий" (парадоксов) Зенона заключалась в том, что бегун, прежде чем добежать до конца дистанции, должен добежать до ее середины, а до этого - до середины половины дистанции и т.д., т.е. должен побывать в бесконечно многих точках, а сделать это за конечное время невозможно. Таким образом, бегун никогда не добежит до конца дистанции! Аполлонию Пергскому, великому современнику Архимеда, мы обязаны созданием теории кривых, которые получаются при сечении конуса плоскостью. Ныне трудно оценить искусство, которое было необходимо для изучения всех фокальных и центральных свойств "конических сечений" с помощью построений циркулем и линейкой. Нам остается только констатировать, что с переходом к современным методам исследований осталось открыть лишь очень немногие свойства сечений (см. также КОНИЧЕСКИЕ СЕЧЕНИЯ). С именем последнего из греческих геометров Паппа Александрийского (ок. 250 - ок. 300) связана одна знаменитая теорема, утверждающая, что если точки А, В, С лежат на прямой l, а точки Аў, Вў, Сў - на прямой lў, то точки пересечения L, M и N прямых АВў и АўВ, прямых АСў и АўC и прямых ВСў и ВўС соответственно лежат на одной прямой (рис. 3). Это свойство точек и прямых не зависит от длины и расстояний; доказав свою теорему, Папп перебросил мост между греческой эпохой и начавшейся в 17 в. новой эрой великих математических открытий (см. также ПРОЕКТИВНАЯ ГЕОМЕТРИЯ).

Рис. 3. ТЕОРЕМА ПАППА.
Аналитическая геометрия. В Средние века Средиземноморская цивилизация постепенно распространилась на север и на запад, но серьезный интерес к математике так и не возродился вплоть до 17 в. Знаменитая Александрийская библиотека пострадала от пожара в 47 до н.э., поэтому о развитии греческой математики до нас дошли только отрывочные сведения. И хотя, несомненно, очень многое оказалось утраченным, не все было так уж плохо, поскольку греческому подходу свойственны определенные внутренние ограничения, на преодоление которых потребовалось бы время. В частности, именно в период между античностью и 17 в. арабы, опираясь на идеи математиков Древнего Вавилона и Индии, развили алгебраическую символику, которая, будучи соединенной с греческой геометрией в трудах П. Ферма (1601-1665) и Р. Декарта (1596-1650) позволила вдохнуть в геометрию новую жизнь. По-видимому, сама идея описания положения точки на плоскости путем соотнесения ее с двумя прямоугольными координатными осями была довольно старой, но мысль о том, что любую точку Р плоскости можно обозначить ее прямоугольными или "декартовыми" координатами (х1, х2) и интерпретировать уравнение f (x1, x2) = 0 как уравнение, задающее плоскую кривую, несомненно, была революционной. Аналогично, в пространстве мы можем обозначить любую точку тремя координатами (x1, x2, x3), уравнением f (x1, x2, x3) = 0 задать поверхность, а системой уравнений

- линию пересечения двух поверхностей в пространстве. В "аналитической" геометрии число координат называется "размерностью" пространства. Наряду с евклидовой геометрией, возникшей в качестве модели внешнего мира, можно рассматривать и абстрактную, не имеющую прямого к нему отношения геометрию пространства n измерений, где n - любое целое положительное число. В таком n-мерном пространстве точка определяется n координатами (x1, x2, x3, ..., xn) и уравнение f (x1, x2, x3, ..., xn) = 0 задает некоторое (n - 1)-мерное геометрическое место точек. Обобщая, можно сказать, что система из r уравнений, где r Ј n, задает (n - r)-мерное геометрическое место точек. Если оси координат взаимно перпендикулярны, то расстояние между двумя точками P (x1, x2, x3, ..., xn) и Q (y1, y2, y3, ..., yn) определяется обобщенным соотношением Пифагора

Из других обобщений теоремы Пифагора выводятся тригонометрические функции. Теперь мы располагаем всем необходимым, чтобы ввести понятие вектора AB как направленного отрезка с началом в точке А и концом в точке В (см. также ВЕКТОР). Аналогично случаю треугольника, местонахождение вектора в пространстве неважно: вектор можно смещать при условии, что его величина и направление остаются неизменными. Величина вектора AB обозначается символом |АВ| и равна расстоянию между точками А и В. Если точки А и В имеют координаты (a1, a2, a3) и (b1, b2, b3), и мы запишем, что

то

Направление вектора AB определяется углами, которые он образует с осями координат. Обозначим эти углы a1, a2, a3. Тогда (рис. 4)
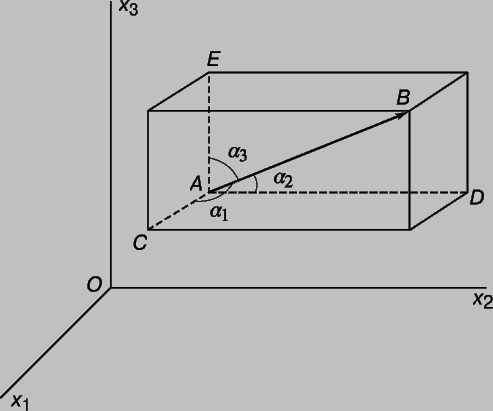
Рис. 4. ОСИ КООРДИНАТ. Отрезок АВ - вектор, величина которого определяется его длиной, а направление - углами a1, a2, a3.

Это т. н. "направляющие косинусы" прямой АВ. Выясним теперь, как выглядит уравнение плоскости p, проходящей через данную точку Q (y1, y2, y3) и перпендикулярной вектору с координатами l1, l2, l3. Из требования, чтобы точка P (x1, x2, x3) лежала в плоскости p, следует, что отрезок PQ перпендикулярен этому вектору, поэтому геометрическое место таких точек задается линейным уравнением

Обратно, любое линейное относительно х1, х2, х3 уравнение определяет некоторую плоскость. Из формулы для расстояния между точками мы получаем уравнение сферы радиуса r с центром в точке Q вида

Общее уравнение второго порядка относительно х1, х2, х3 задает поверхности второго порядка, или т.н. квадрики (если только оно не "факторизуется", т.е. не вырождается в произведение двух линейных множителей, задающих две плоскости). Квадрики бывают семи типов: цилиндр, конус, эллипсоид, однополостной гиперболоид, двуполостной гиперболоид, эллиптический параболоид и гиперболический параболоид. С помощью подходящего выбора координатных плоскостей уравнения центральных квадрик (эллипсоидов и гиперболоидов) можно привести к нормальному виду:

где а1, а2, а3 - длины "главных полуосей"; эти поверхности симметричны относительно начала координат, которое служит центром квадрик. Хотя параболоиды не имеют центров симметрии, за нормальные формы их уравнений можно принять следующие:

(гиперболический параболоид). Некоторые из этих поверхностей являются линейчатыми. Это означает, что через каждую точку такой поверхности можно провести по крайней мере две прямые, целиком лежащие на этой поверхности; в результате получим два семейства прямых, любое из которых образует всю поверхность. Эти прямые называют образующими. Если мы ограничимся рассмотрением какой-нибудь одной плоскости, например, положив для этого в уравнении квадратичной поверхности x3 = 0, то получим уравнения конических сечений - кривых, по которым эти поверхности пересекают плоскость x3 = 0. Это - эллипс (частным случаем которого является окружность), гипербола и парабола">
(эллиптический параболоид)

(гиперболический параболоид). Некоторые из этих поверхностей являются "линейчатыми". Это означает, что через каждую точку такой поверхности можно провести по крайней мере две прямые, целиком лежащие на этой поверхности; в результате получим два семейства прямых, любое из которых образует всю поверхность. Эти прямые называют образующими. Если мы ограничимся рассмотрением какой-нибудь одной плоскости, например, положив для этого в уравнении квадратичной поверхности x3 = 0, то получим уравнения конических сечений - кривых, по которым эти поверхности пересекают плоскость x3 = 0. Это - эллипс (частным случаем которого является окружность), гипербола и парабола
