Akademik

- 1) Г. т. о базисе: если А - коммутативное нётерово кольцо и 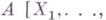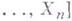- кольцо многочленов от с коэффициентами в А, то и 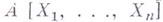- нётерово кольцо. В частности, в кольце многочленов от конечного числа переменных над полем или над кольцом целых чисел любой идеал порождается конечным числом элементов (имеет конечный базис). Именно в такой форме теорема была доказана Д. Гильбертом [1] и играла вспомогательную роль в доказательстве основной Гильберта теорема об инвариантах. Впоследствии Г. т. о базисе получила широкое распространение в коммутативной алгебре.

Лит.:[1] Нilbеrt D., "Math. Ann.", 1890, Bd 36, S. 473- 534. В. И. Данилов.

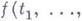
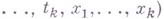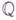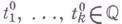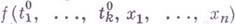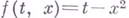2).Г. т. о неприводимости: пусть - неприводимый многочлен над полем рациональных чисел ; тогда существует бесконечное множество значений переменных при к-рых многочлен неприводим над . Так, многочлен остается неприводимым для всех 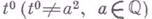и только для них. Полученная Д. Гильбертом (D, Hilbert) в 1892, эта теорема обобщалась затем на случай многочленов над нек-рыми другими полями (напр., над полем конечного типа над своим простым подполем [2]).

Г. т. о неприводимости применяется в исследованиях, связанных с Галуа теории обратной задачей и алгебраических многообразий арифметикой. Пусть над полем 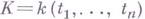рациональных функций от существует такое расширение 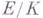с группой Галуа 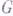, что поле kалгебраически замкнуто в Еи к нему применима Г. т. о неприводимости. Тогда можно так выбрать значения переменных в поле k, что получающееся расширение поля kбудет иметь группой Галуа группу G. Используя это соображение, Д. Гильберт построил в [1] расширения поля с симметрической и знакопеременной группами. При этом, в случае симметрич. группы за Еберется поле рациональных функции от ппеременных, а в качестве 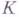- подполе поля сим-метрич. функций, к-рое само будет полем рациональных функций. Обобщая этот подход, Э. Нётер (Е. Noether) рассмотрела произвольную подгруппу п расширение Есоответствующего поля инвариантов Еотносительно группы G(см. [3]). Г. т. о неприводимости дает возможность построить расширение поля kс группой Галуа G, если только поле 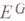есть поле рациональных функций над 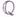. Вопрос о выполнимости последнего условия (проблема Нётер), тесно связан с Люрота проблемой. Лишь в 1969 Р. Суон (R. Swan) показал, что в общем случае ответ на него отрицательный (см. [4], [6]).

Г. т. о неприводимости применяется также при построении рациональных точек абелевых многообразий Анад полем рациональных чисел . В силу теоремы Мор-делла - Вейля группа рациональных точек Аявляется конечно порожденной, и возникает вопрос о значении ее ранга г. Используя Г. т. о неприводимости, А. Нерон (A. Neron) построил многообразия Аразмерности 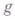и ранга больше или равного 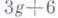(см. [2]).

Лит.:[1] Нilbеrt D., "J. reine und angew. Math.", 1892, Bd 110, S. 104-29; [2] Lang S., Diophantine Geometry, N. Y., 1962; [3] Чеботарев Н. Г., Теория Галуа, М.- Л.. 1936, с. 18-32. 90-94; [4] Martinet J., "Seminaire Bourbaki", 1969/1970, В., 1971; [5] Sсhinzеl А., в кн: "Actes du Congr?s International des Mathematiciens", t. 1, P., 1971; [C] Воскресенский В. Е., "Тр. Матем. ин-та АН СССР", 1973, т. 82, с. 151-61. А. Н. Паршин.

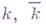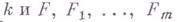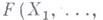
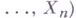3) Г. т. о нулях (о корнях): пусть k - поле, - кольцо многочленов над - алгебраич. замыкание поля - многочлены из .Корнем многочлена наз. последовательность элементов из k, удовлетворяющая условию 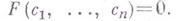Если каждый общий корень многочленов является корнем многочлена 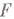, то существует такое целое число 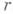, зависящее только от 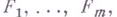что 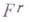принадлежит идеалу, порожденному 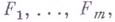то есть

где - нек-рые многочлены. Получена Д. Гильбертом [1].

Г. т. эквивалентна утверждению, что для любого собственного идеала а кольца существует корень, общий для всех многочленов из а. Таким образом, Г. т. может рассматриваться как далеко идущее обобщение основной теоремы алгебры. На Г. т. можно смотреть и как на утверждение о том, что любой простой идеал кольца является пересечением максимальных идеалов, его содержащих; это приводит к понятию Джекобсона кольца.

При геометрич. интерпретации корни идеала соответствуют алгебраич. точкам аффинного многообразия, определяемого идеалом п.

Из Г. т. следует, что на любом непустом аффинном многообразии имеется алгебраич. точка. Таким образом, множество алгебраич. точек всюду плотно на многообразии, и потому однозначно его определяет - причина, по к-рой при изучении алгебраич. многообразия часто ограничиваются алгебраич. точками.

Лит.: [1] Нilbеrt D., "Math. Ann.", 1893, Bd 42, S. 313- 73; [2] Ван - дер - Варден Б. Л., Современная алгебра, пер. с нем., ч. 2, 2 изд., М.- Л., 1947; [3] 3арисский О., Самюэль П., Коммутативная алгебра, пер. с англ., т. 2, М., 1963; [4] Ленг С., Алгебра, пер. с англ., М., 1968; [5] Бурбаки Н., Коммутативная алгебра, пер. с франц., М., 1971. В. И. Данилов.

4) Г. т. о поверхностях отрицательной кривизны: в трехмерном евклидовом пространстве не существует полной регулярной поверхности постоянной отрицательной кривизны. Доказана Д. Гильбертом (D. Hilbert, 1901; см. [I]).

Лит.:[1] Гильберт Д., Основания геометрии, пер. с нем., М.-Л., 1948. Е. В. Шикин.

5) Г. т. о сизигиях- теорема о конечности цепи сизигий градуированного модуля над кольцом многочленов (в класснч. формулировке см. [I]).

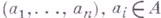Пусть А - нётерово кольцо, М - нётеров A-модуль, и - система образующих модуля М. Модулем сизпгпй (соотношений) S(М).модуля Мназ. модуль соотношений для т. е. A-модуль векторов , удовлетворяющих условию: 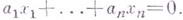Индуктивно определяется i-й модуль сизигии 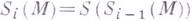модуля 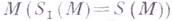.Иначе это можно описать с помощью точной последовательности, наз. цепью сизигий:

где - свободные A-модули конечного типа. В современном изложении Г. т. о сизигиях допускает следующую формулировку : если А - локальное регулярное кольцо размерности т, то m-й модуль сизигий любого нётерова А-модуля является свободным модулем. Это эквивалентно тому, что любой A-модуль имеет свободную резольвенту длины т, или что Аимеет глобальную проективную размерность т. Это свойство характеризует регулярные кольца [2].

Глобальный вариант Г. т. о сизигиях: над регулярным кольцом А(напр., над кольцом многочленов) любой A-модуль конечного типа имеет проективную (но уже не обязательно свободную) резольвенту конечной длины.

Лит.:[1] Нilbеrt D., "Math. Ann.", 1890, Bd 36, S. 473- 534; [2] Serre J.-P., в кн.; Proceedings of the International - Symposium on Algebraic Number Theory, Tokyo, 1955, p. 175-89; [З] Серр Ж.-П., "Математика", 1963, т. 7, № 5, с. 3-93; [4] 3арисский О.. Самюэль П., Коммутативная алгебра, пер. с англ., т. 2, М., 1963. В. И. Данилов.

6) Г. т. о циклических расширениях (теорема Гильберта 90): пусть K - циклич. расширение с циклической группой Галуа 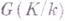поля 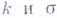- образующая группы 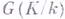; тогда норма 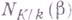элемента 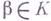равна единице в том и только в том случае, если существует ненулевой элемент 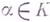удовлетворяющий условию 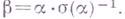Аналогично, след 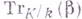равен нулю тогда и только тогда, когда 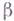может быть представлено в виде 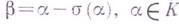(см. [1], [2], [3]).

Г. т. может рассматриваться как следствие более общего утверждения о когомологиях групп Галуа (см. [4]). Именно: если K - расширение Галуа группы kс группой Галуа G, то мультипликативная группа 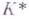поля K превращается в G-модуль, и первая группа ко-гомологий 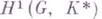равна нулю. Аналогично,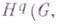 при (см. Галуа когомологии).

Другим обобщением Г. т. является теория спуска Гротендика; одно из применений ее в этальной топологии, также известное под назв. "теорема Гильберта 90", утверждает, что этальные когомологии 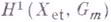схемы 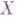со значениями в пучке мультипликативных групп 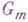изоморфны группе Пикара 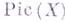классов обратимых пучков на .

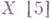Лит.:[1] Нilbеrt D., "Jahresbericht der D. М. V.", 1897, Bd 4, S. 175-546; [2]Ленг С., Алгебра, пер. с англ., М., 1968; L3] Бурбаки Н., Алгебра. Многочлены и поля. Упорядоченные группы, пер. с франц., М,, 1965; [4] Серр Ж.-П., Когомологии Галуэ, пер. с франц., М., 1968: [5] Аrtin М., Grothendieck A., Cohomoloprie Stale des schcmas, Serainaire IHES, 1963-64. В. И. Данилов.

7) Г. т. о существовании абсолютного экстремума: пусть

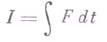
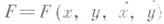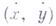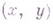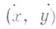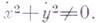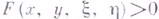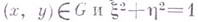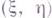есть функционал вариационной задачи в параметрич. форме, где - положительно определенная функция 1-й степени по , трижды непрерывно дифференцируемая по всем аргументам для всех из области Gи всех , удовлетворяющих условию Кроме того, предполагается, что для всех (т. е. функционал / положительно определен), а также, что множества строго выпуклы по для всех 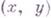из выпуклой замкнутой подобласти 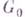(т. е. функционал I регулярен, или эллиптичен).

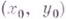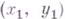При этих предположениях для любых двух точек и из 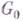найдется кривая, доставляющая функционалу I абсолютный минимум среди всех спрямляемых кривых.

Г. т. получена Д. Гильбертом (D. Hilbert, 1899).

Лит.:[1] Ахиезер Н. И., Лекции по вариационному исчислению, М., 1955. В. М. Тихомиров.

8) Г. т. об инвариантах- теорема, устанавливающая конечнопорожденность алгебры всех многочленов на комплексном векторном пространстве форм степени dот rпеременных, инвариантных относительно действия полной линейной группы 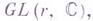определяемого линейными заменами этих переменных. Первое доказательство теоремы, использующее Гильберта теорему о базисе и формальные процессы инвариантов теории, дано в [1]. Д. Гильберт [2] конструктивно доказал эту теорему и получил оценку сверху для степеней образующих указанной алгебры инвариантов (что, в принципе, дает возможность их выписать явно). Г. т. является первой основной теоремой теории инвариантов для d- йсимметрич. степени стандартного представления 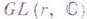. Доказательство Г. т. стимулировало постановку вопроса о конечнопорожденности алгебр инвариантов для подгрупп группы 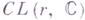а также постановку 14-й проблемы Гильберта. Используя теорию интегрирования на группах, Г. Вейль (Н. Weyl) доказал конечнопорожденность алгебры инвариантов для любых конечномерных представлений компактных групп Ли и комплексных полупростых групп Ли (см. [3]).

Г. т. принято называть также следующее ее обобщение: если R - алгебра конечного типа над полем k, G - геометрически редуктивная группа ее k-автоморфизмов и 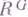- подалгебра всех G-инвариантных элементов в R, то 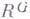также имеет конечный тип над k(см. [4], [5]).

Лит.:[1] Hilbert D., "Math. Ann.", 1890, Bd 36, S. 473-534; [2] его же, "Math. Ann.", 1893, Bd 42, S. 313-73: [3] Вейль Г., Классические группы, их инварианты и представления, пер. с англ., М., 1947; [4] Mumford D., Geometric invariant theory, B.-Hdlb.-N.Y., 1965; [5] Nagata M., "J. Math. Kyoto Univ.", 1963/64, v. 3. В. Л. Попов.