Akademik

в пространстве r-мерных полиэдральных цепей С _r( Е ^п) - наибольшая из полунорм 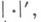удовлетворяющих для любой клетки s^r объема |s^r| неравенствам:

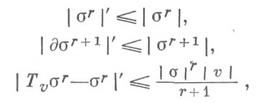
где T_vs^r - клетка, полученная сдвигом на вектор длины |u|.

Если А = е а _is_i^r, то Д. н. А* выражается так:

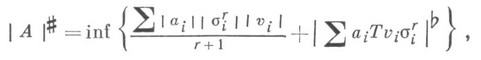
где | С|^b- бемольная норма цепи С.

Имеет место:

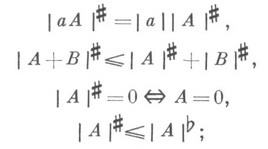
если r=0, то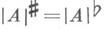

Пополнение пространства С _r( Е ^п). является сепарабельным банаховым пространством 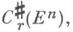элементы к-рого наз. r-мерными диезными цепями. Для любой r-мерной полиэдральной цепи Аи любого вектора vимеет место

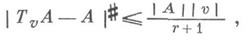
где T_vA- цепь, полученная сдвигом Ана вектор vдлины |v|. Бемольная цепь конечной массы является диезной цепью; вообще любую бемольную цепь можно рассматривать и как диезную цепь в таком смысле: если 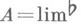А _i, где A_i- полиэдральные цепи, и 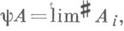где y.- линейное биективное отображение пространства 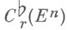в пррстранствои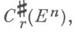 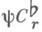плотно в 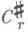при Д. н.

Дать корректное определение границы дА диезной цепи невозможно (см. [1], с. 242, пример (с)); r-мерная диезная коцепь Х=ХА есть элемент пространства 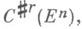сопряженного к она является бемольной коцепью, причем 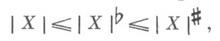где |Х| - ко масса X, а диезная конорма 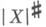определяется аналогично бемольной норме | Х|^b. Кограница dX диезной коцепи не обязана быть диезной ([1], с. 241, пример (а)), однако

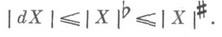
Константа Липшица 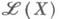коцепи Xопределяется следующим образом:

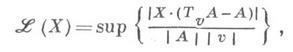
где А - полиэдральные цепи. Для диезных коцепей эта верхняя грань конечна и

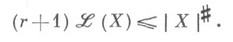
Любая бемольная коцепь с конечной константой Липшица является диезной, причем

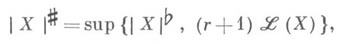
и, кроме того,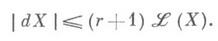

Аналогичные понятия вводятся для r-мерных полиэдральных цепей в открытых подмножествах 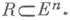См. также Диезная форма.

Диезная норма в пространстве аддитивных функций у, значениями к-рых являются r- векторы,- наибольшая из полунорм |Х|', удовлетворяющих условиям:

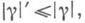где | у|- полная вариация g;

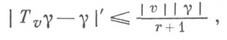
где T_vg(Q)=gT_-v(Q).- сдвиг функции уна вектор vдлины |v|:T__v(Q) = {q-v, q ОQМ Eⁿ};. для каждой точки ри любого е существует h>0 такое, что 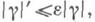если носитель sp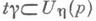и у( Е ^п)=0.

Д. н. 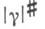имеет представление

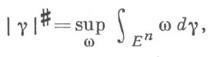
где w - r-мерные диезные формы, для к-рых

Лит. см. при статье Бемольная норма.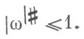

М. И. Войцеховский.