Akademik

- обыкновенное дифференциальное уравнение

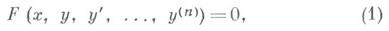
левая часть к-рого может быть записана в виде полной производной:

Другими словами, уравнение (1) является Д. у. в п. д., если существует такая дифференцируемая функция Ф( х, и ₀, и ₁, . .., и _п_₁), что

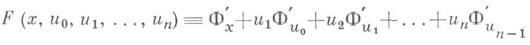
тождественно по всем аргументам. Решение уравнения n-го порядка в полных дифференциалах сводится к решению 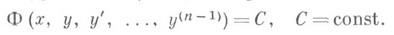уравнения (n-1)-го порядка

Пусть F(x, и ₀, и ₁,. . ., и _n) есть праз непрерывно дифференцируемая функция, а Ф ( х, и ₀, и ₁,..., и _п-1)- функция, имеющая непрерывные частные производные до 2-го порядка включительно. Пусть

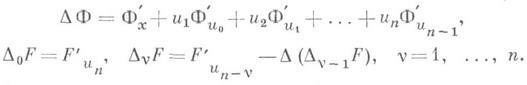
Для того чтобы уравнение (1) было Д. у. в п. д., достаточно, чтобы функции D_vF, v=0, 1, ..., п, не зависели от и _п и D_nF=0 (см. [1]). В частности, и _п может входить в Fтолько линейно. Уравнение 1-го порядка

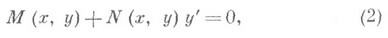
где функции М, N, M'_y, n'_x определены и непрерывны в открытой односвязной области Dплоскости ( х, у )и М ²+N²>0 в D, будет Д. у. в п. д. в том и только в том случае, когда

Общее решение уравнения (2) в полных дифференциалах имеет 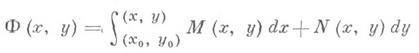вид Ф{х, у)=0, где и интеграл берется по любой спрямляемой кривой, лежащей в области Dи соединяющей произвольную фиксированную точку 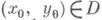с точкой ( х, у )(см. [2]). Уравнение (2) (в общем случае уравнение (1), линейное по y⁽ⁿ⁾) может быть приведено (при нек-рых предположениях) к Д. у. в п. д. умножением на интегрирующий множитель.

Лит.:[1] К амк е Э., Справочник по обыкновенным дифференциальным уравнениям, пер. с нем., 5 изд., М., 1976; [2] Еругин Н. П., Книга для чтения по общему курсу дифференциальных уравнений, 2 изд., Минск, 1972.

Н. X. Розов.