Akademik

- теоретико-информационная мера возможности передачи информации по каналу связи.. Пусть hи 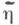- случайные величины, связанные каналом связи (Q, V) . К. п. с. Стакого канала определяется равенством

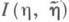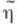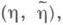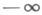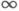где - информации количество в относительно h, а верхняя грань берется по всем парам случайных величин связанным каналом (Q, V). В случае, когда сигналы на входе и выходе канала h={h(t), <t<} и 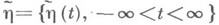являются случайными процессами с непрерывным или дискретным временем, под К. п. с. обычно понимают среднюю К. п. с, приходящуюся на единицу времени или на один символ передаваемого сигнала, т. е., по определению, полагают

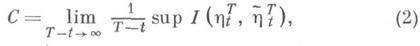
если такой предел существует; здесь верхняя грань берется по всевозможным парам случайных величин

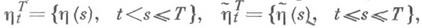связанных соответствующим отрезком данного канала. Существование предела (2) доказано для достаточно широкого класса каналов, напр, для однородных каналов с конечной памятью и необращающимися в нуль вероятностями перехода.

Известно, что в достаточно широком классе случаев (напр., для упомянутых выше каналов с конечной памятью) справедливо равенство

где верхняя грань берется по всем парам стационарно связанных случайных процессов h(t),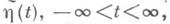 таким, что при любых 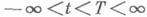случайные величины 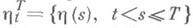и 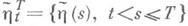связаны соответствующим отрезком рассматриваемого канала. Равенство (3) показывает, таким образом, что К. п. с. совпадает с максимально возможной информации скоростью передачи по этому каналу.

Явное вычисление К. п. с. оказывается возможным лишь в ряде частных случаев, напр, для каналов симметричных без памяти и каналов гауссовских. Поэтому значительный интерес представляют различные асимптотические формулы для К. п. с. Напр., для канала (Q, V), сигналы на входе и выходе к-рого принимают значения в га-мерном евклидовом пространстве Rⁿ, переходная функция канала 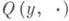задается плотностью 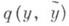(относительно меры Лебега), у,и ограничение Vсостоит в ограничении на среднюю мощность сигнала на входе 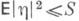(где h - длина вектора h в Rⁿ), S>0 - фиксированное число, известны следующие результаты (см. [1]).

1) Пусть т. е. рассматривается канал с аддитивным шумом, так что сигнал на выходе h равен сумме 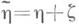сигнала на входе h. и не зависящего от него шума z, и пусть 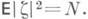Тогда при 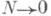(при слабых дополнительных условиях) справедлива асимптотическая формула

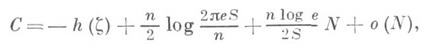
где h(z).- дифференциальная энтропияz, а о 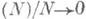при Эта формула соответствует случаю малого шума.

2) Пусть 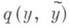- произвольно, но Тогда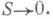

где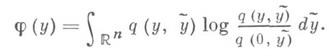

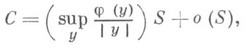
Лит.:[1] Прелов В. В., "Пробл. передачи информ.", 1969, т. 5, № 2, с. 31 - 36; 1972, т. 8, № 4, с. 22-27.

См. также [1], [3]-[6] при ст. Канал связи.

Р. Л. Добрушин, В. В. Прелов.