Akademik

о равномерном приближении целыми функциям и: для того чтобы для любой непрерывной комплексной функции f(z) на континууме Еи произвольно быстро убывающей при положительной функции e(r), 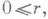нижняя грань к-рой на любом конечном интервале положительна, существовала целая функция g(z)такая, что

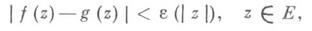
необходимо и достаточно, чтобы Ене содержал внутренних точек и существовала растущая к 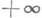функция h(t),такая, что любую точку z дополнения СЕ можно соединить с оо жордановой кривой, расположенной вне Еи вне круга |z|<h(|z|).

Этот результат М. В. Келдыша и М. А. Лаврентьева [1] подвел итог многочисленным исследованиям по приближениям целыми функциями, начатым Карлемана теоремой (п. 3, см. также [2]).

Лит.:[1] Келдыш М. В., Лаврентьев М. А., "Докл. АН СССР", 1939, т. 23, № 8, с. 746 - 48; 12] Мергелян С. Н., "Успехи матем. наук", 1952, т. 7, в. 2, с. 31 - 112.

Е. Д. Соломенцев.