Akademik

приближение дифференциального оператора таким зависящим от параметра оператором, результат применения к-рого к функции определяется ее значениями на нек-ром дискретном множестве точек - сетке, уточняющееся при стремлении параметра (шага сетки) к нулю.

Пусть 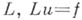- дифференциальный оператор, переводящий каждую функцию ииз класса функций 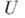в функцию 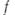из линейного нормированного пространства F. Пусть 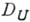- область определения функций из 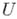и в 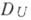выделено нек-рое дискретное подмножество - сетка 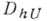("сгущающаяся" при 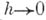). Рассматривается множество 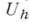всех функций 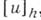, определенных только на сетке и совпадающих в точках сетки с и. Разностным оператором наз. всякий оператор 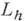, переводящий сеточные функции из 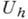в функции 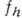из F. Говорят, что оператор 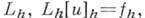аппроксимирует (аппроксимирует с порядком 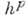) дифференциальный оператор Lна классе U, если для любой функции uОU при h->0

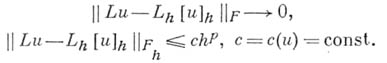
Иногда аппроксимацию понимают как равенство

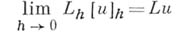
в смысле той или иной слабой сходимости. А. д. о. р. используется для приближенного вычисления функции Lu по таблице [и]_h значений функции ии для аппроксимации дифференциального уравнения разностным.

Существуют два основных приема построения оператора L_h , аппроксимирующего L.

Первый состоит в том, что определяют 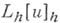как результат применения дифференциального оператора Lк функции из 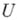, полученной с помощью той пли иной интерполяционной формулы из сеточной функции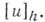

Второй способ состоит в следующем. В области 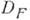определения функции f из Fвводят сетку 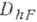и рассматривают линейное пространство 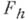сеточных функций, определенных на 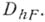Оператор 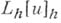строят как произведение двух операторов: оператора, переводящего функцию 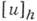в сеточную функцию 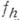из 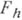, то есть в приближенную таблицу значений функции 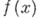, и оператора восполнения 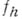с сетки 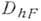на всю область 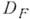. Напр., для приближения оператора дифференцирования

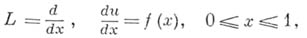
строится сетка 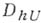, состоящая из точек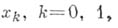

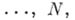
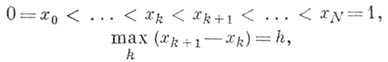
и сетка D_{h F} состоящая из точек

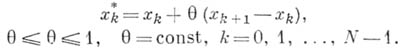
Значения оператора L_h[u]_h в точках х _k^* определяются равенствами

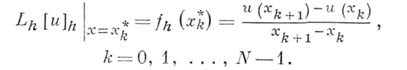
Затем 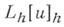доопределяется вне 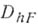кусочно линейно с 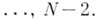изломами, быть может, только в точках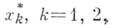

Пусть норма в 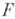определяется формулой

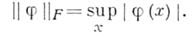
Тогда на классе функций 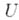, имеющих ограниченную третью производную, при 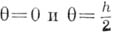оператор 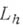аппроксимирует 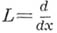с порядком 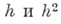соответственно.

На классе 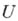функций с ограниченными вторыми производными аппроксимация при любом 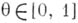имеет лишь первый порядок.

Иногда задачу А. д. о. р. условно считают решенной, если указан способ построения сеточной функции

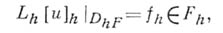
определенной только в точках сетки 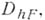оставляя задачу о восполнении функции 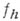всюду на 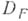вне рассмотрения. В таком случае для определения аппроксимации пространство 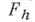считают нормированным и притом относительно сетки п нормы предполагается, что для всякой функции 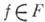совпадающая с ней в точках 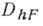функция 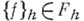удовлетворяет равенству

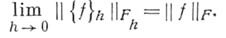
Оператор 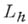понимают как оператор из 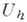в 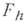и говорят, что оператор 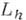аппроксимирует (аппроксимирует с порядком 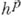) дифференциальный оператор 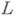на множестве 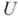, если при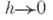

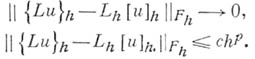
Для построения оператора 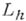, аппроксимирующего 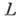на достаточно гладких функциях с заданным порядком, часто прибегают к замене каждой производной, входящей в выражение 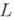, ее разностной аппроксимацией, опираясь для этого на следующий факт. При любых натуральных 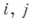и при любом 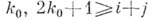в равенстве

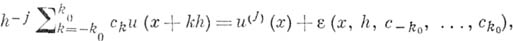
используя метод неопределенных коэффициентов и формулу Тейлора, можно так подобрать числа 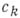, не зависящие от h., чтобы для любой функции 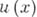, имеющей 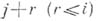ограниченных производных, выполнялось веравенство вида

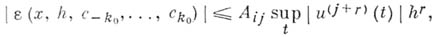
где 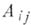зависит только от 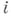и 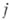. Напр., пусть требуется построить аппроксимирующий оператор для оператора Лапласа

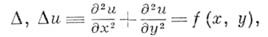
если 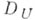- замкнутый квадрат 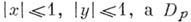- его внутренность 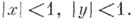Задается 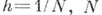- натуральное, и строится сетка, причем к D_hU относятся точки

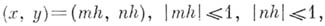
а к 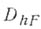- точки

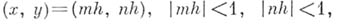
где 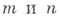- целые. Так как

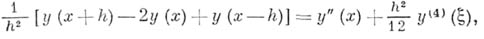
то 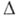на достаточно гладких функциях аппроксимируется со вторым порядком разностным оператором 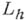, если положить в точках D_hF

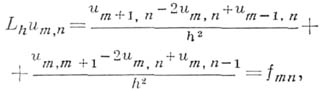
где 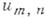и 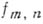- значения функци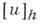й и 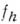в точке (mh, nh).

Существуют отличные от указанного способы построения операторов 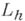, аппроксимирующих оператор Lна решениях 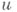дифференциального уравнения Lu=0 и удовлетворяющих дополнительным требованиям.

Лит.:[1] Филиппов А. Ф., "Докл. АН СССР", 1955, т. 100, Лс 6, с. 1045-48; [2] Березин И. С., Жидко в Н. П., Методы вычислений, 3 изд., т. 1, М., 1966. В. С. Рябенъкий.