Akademik

точки, в к-рых действительная функция принимает наибольшее или наименьшее значения на области определения; такие точки наз. также точками абсолютного максимума или абсолютного минимума. Если функция f определена на топологич. пространстве X, то точка х ₀ наз. точкой локального максимума (локального минимума), если существует такая окрестность 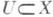точки х ₀, что для сужения рассматриваемой функции на этой окрестности точка х ₀ является точкой абсолютного максимума (минимума). Различают точки строгого и нестрогого максимума (мини м у м а) (как абсолютного, так и локального). Напр., точка наз. точкой нестрогого (строгого) локального максимума функции f, если существует такая окрестность точки х ₀, что для всех выполняется неравенство 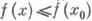(соответственно f(х)<f(x₀). )/

Для функций, определенных на конечномерных областях, в терминах дифференциального исчисления существуют условия и признаки того, чтобы данная точка была точкой локального максимума (минимума). Пусть функция f определена в нек-рой окрестности тючки x₀ числовой оси. Если x₀- точка нестрогого локального максимума (минимума) ив этой точке существует производная f'(x₀), то она равна нулю.

Если заданная функция f дифференцируема в окрестности точки x₀, кроме, быть может, самой этой точки, в к-рой она непрерывна, и производная f' по каждую сторону от точки x₀ в этой окрестности сохраняет постоянный знак, то для того чтобы x₀ была точкой строгого локального максимума (локального минимума), необходимо и достаточно, чтобы производная меняла знак с плюса на минус, т. е. чтобы f' (x)>0 при x<.x₀ и f'(x)<0 при x>x₀ (соответственно с минуса на плюс: f' (х)<0 при x<x₀ и f'(x)>0 при х>х ₀). Однако не для всякой функции, дифференцируемой в окрестности точки x₀, можно говорить о перемене знака производной в этой точке. . '

Если функция fимеет в точке х ₀ т производных, причем то для того чтобы х ₀ была точкой строгого локального максимума, необходимо и достаточно, чтобы те было четным и чтобы f^(m)(x₀)<0, и - локального минимума, чтобы m было четно и f^(m) (x₀)>0.

Пусть функция f(x₁ ..., х _п]определена в n-мерной окрестности точки 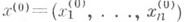и дифференцируема в этой точке. Если x⁽⁰⁾ является точкой нестрогого локального максимума (минимума), то дифференциал функции f в этой точке равен нулю. Это условие равносильно равенству нулю в этой точке всех частных производных 1-го порядка функции f. Если функция имеет 2-е непрерывные частные производные в точке x⁽⁰⁾, все ее 1-е производные обращаются в x⁽⁰⁾ в нуль, а дифференциал 2-го порядка в точке x⁽⁰⁾ представляет собой отрицательную (положительную) квадратичную форму, то x⁽⁰⁾ является точкой строгого локального максимума (минимума). Известны условия для М. и м. т. дифференцируемых функций, когда на область изменения аргументов наложены определенные ограничения: удовлетворяются уравнения связи. Необходимые и достаточные условиям максимума (минимума) действительной функции, область определения к-рой имеет более сложную структуру, изучаются в специальных разделах математики: напр., в выпуклом анализе, математическом программировании (см. также Максимизация и минимизация функций). М. и м. т. функций, определенных на многообразиях, изучаются в вариационном исчислении в целом, а М. и м. т. для функций, заданных на функциональных пространствах, т. е. для функционалов, в вариационном исчислении. Существуют также различные методы численного приближенного нахождения М. и м. т.

Лит.:[1] И л ь и н В. А., П о з н я к Э. Г., Основы математического анализа, 3 изд., ч. 1,М., 1971; [2] КудрявцевЛ. Д., Курс математического анализа, т. 1,2, М., 1981; [3] Никольский С. М., Курс математического анализа, 2 изд., т. 1, М., 1975; [4] Б а х в а л о в Н. С., Численные методы, 2 изд., т. 1, М., 1975. Л. Д. Кудрявцев.