Akademik

- наибольший из общих делителей целых, в частности натуральных, чисел . Если данные числа не все равны нулю, то такой делитель существует. Н. о. д. чисел обычно обозначают символом

Свойства Н. о. д.:

1) Н. о. д. чисел делится на любой общий делитель этих чисел;

2)

3) если целые числа представлены в виде

где - различные простые,

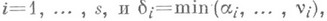то

Н. о. д. двух натуральных чисел можно найти при помощи Евклида алгоритма. Число шагов, необходимых для отыскания Н. о. д. двух чисел, превосходит не более чем в пять раз число цифр наименьшего из них, записанного в десятичной системе счисления.

Н. о. д. элементов области целостности наз. тот из общих делителей данных элементов, к-рый делится на любой из их общих делителей. Так, Н. о. д. двух многочленов над данным полем - тот их общий делитель, к-рый делится на любой из их общих делителей. Если Н. о. д. двух элементов области целостности существует, то он единствен с точностью до обратимого множителя. Н. о. д. идеалов данного кольца наз. идеал порожденный объединением множеств (см. Факториалъное кольцо).

Лит.:[1] Виноградов И. М., Основы теории чисел, 9 изд., М., 1981; [2] Бухштаб А. А., Теория чисел, 2 изд., М., 1966; [3] Маркушевич А. И., Деление с остатком в арифметике и алгебре, М.- Л., 1949; [4] Фор Р., Кофман А., Дени-Папен М., Современная математика, пер. с франц., М., 1966; [5] Ленг С, Алгебра, пер. с англ., М., 1968.

А. А. Вухштаб, В. И. Нечаев.