Akademik

- интеграл

от заданной функции одного переменного, определенной на нек-ром промежутке - совокупность всех первообразных данной функции на этом промежутке. Если функция f определена на нек-ром промежутке числовой оси и F- нек-рая ее первообразная на , т. е. 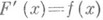для всех 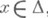, то всякая другая первообразная функция f на имеет вид 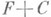, где С- нек-рая постоянная. Следовательно, Н. и. (*) состоит из всевозможных функций вида 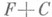. Неопределенным интегралом Лебега от суммируемой на отрезке 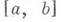функции f наз. совокупность всех функций вида В этом случае равенство 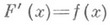выполняется, вообще говоря, лишь почти всюду на отрезке .

Неопределенным интегралом Лебега (в широком смысле) от суммируемой функции f, определенной на измеримом пространстве Xс мерой , наз. функция множеств

определенная на множестве всех измеримых множеств Епространства X.

Лит.:[1] Колмогоров А. Н., Фомин С. В., Элементы теории функций и функционального анализа, 5 изд., М., 1981; [2] Никольский С. М., Курс математического анализа,. 2 изд., т. 1-2, М., 1975; [3] Ильин В. А., Позняк Э. Г., Основы математического анализа, 3 изд., ч. 1, М., 1971.

Л. Д. Кудрявцев.