Akademik

- отображение 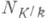поля Kв поле k, где K - конечное расширение поли k, ставящее в соответствие элементу 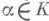элемент 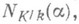являющийся определителем матрицы k-линейного отображения 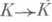, переводящего 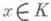в 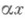. Элемент 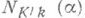наз. нормой элемента a.

Равенство 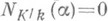выполняется тогда и только тогда, когда 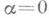. Для любых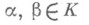

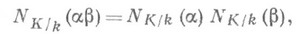
т. е. 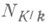индуцирует гомоморфизм мультипликативных групп 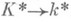, к-рый также наз. норменным отображением. Для любого

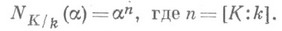
Группа 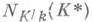наз. норменной подгруппой в 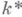, или группой норм (из поля Kв поле k). Если 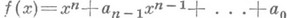- характеристич. многочлен элемента относительно поля k, то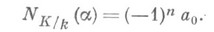

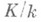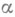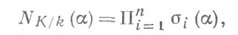Пусть расширение сепарабельно. Тогда для любого из К где 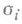- все k-изоморфизмы поля Kв алгебраич. замыкание 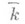поля к. Н. о. обладает свойством транзитивности. Есл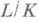и и 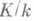- конечные расширения, то 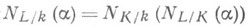для любого 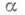из L.

Лит.:[1] Ленг С, Алгебра, пер. с англ., М., 1968; [2] Борсвич 3. И., Шафаревич И. Р., Теория чисел, 2 изд., М., 1972.

Л. В. Кузьмин.