Akademik

(обратный оператор) к однозначному отображению (оператору)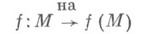- однозначное отображение gтакое, что

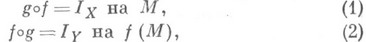
где 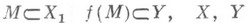- нек-рые множества.

Если gудовлетворяет лишь условию (1), то оно наз. правым обратным отображением к f, если лишь (2) - левым обратным отображением к f. О. о.существует тогда и только тогда, когда для любого ,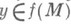полный прообраз состоит из единственного элемента 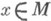. Если отображение f имеет обратное отображение f^-1, то уравнение

однозначно разрешимо при любом . Если существует только правое О. о., то существует и решение уравнения (3), но вопрос об однозначности решения остается открытым. Наличие же лишь левого О. о. обеспечивает единственность решения в предположении, что оно существует. Если Xи Y - векторные пространства, и A - линейный оператор из Xв Y, то А ^-1, если он существует, тоже линеен. Вообще, в случае наделения Xи Y той или иной структурой, случается, что нек-рые свойства оператора Асохраняются и при переходе к 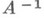в предположении, что он существует. 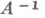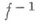Так, если Xи Y - банаховы пространства и - замкнутый оператор, то также замкнут; если Н- гильбертово пространство и самосопряжен, то также самосопряженный оператор; если - нечетная функция, то - также нечетная, и т. д. Непрерывность Ане всегда сохраняется при переходе к для многих важных классов линейных операторов, напр, вполне непрерывных. Важными признаками непрерывности операторов, обратных к линейным, являются следующие.

Пусть X- конечномерное векторное пространство с пек-рым базисом и 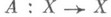задается в этом базисе, матрицей 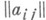. Для существования 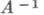необходимо и достаточно, чтобы 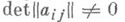(операторы Аи А ^-1 в этом случае автоматически непрерывны).

Пусть Xи Y - банаховы пространства и A - линейный непрерывный оператор из Xв Y.

1) Если 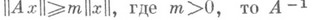существует и непрерывен.

2) Если существует и непрерывен, причем

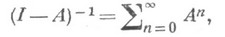
где ряд справа сходится по норме в пространстве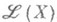

3) Оператор 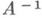существует и непрерывен на всем Y тогда и только тогда, когда его сопряженный имеет обратный, определенный и непрерывный на всем При этом .

4)Если оператор существует и непрерывен и 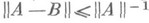, то оператор 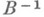также существует и непрерывен, причем

Таким образом, множество обратимых операторов открыто в в равномерной топологии этого пространства.

5) Теорема Банаха об изоморфизме: если Авзаимно однозначно отображает Xна Y, то О. о., к-рое существует, непрерывно. Эта теорема допускает обобщение: взаимно однозначное линейное непрерывное отображение совершенно полного пространства Xна отделимое бочечное пространство Y является топологич. изоморфизмом.

Ряд утверждений о существовании и непрерывности оператора, обратного к линейному непрерывному, содержится в спектральной теории линейных операторов, действующих в гильбертовом пространстве. Так, если Асамосопряжен и 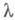не действительно, то 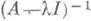существует и непрерывен.

Лит.:[1] Данфорд Н., Шварц Д ж., Линейные операторы. Общая теория, пер. с англ., М., 1962; [2] Канторович Л. В., Акилов Г. П., Функциональный анализ, 2 изд., М., 1977; [3] Рудин У., Функциональный анализ, пер. с англ., М., 1975; [4] Робертсон А.-П., Робертсон В.-Дж., Топологические векторные пространства, пер. с англ., М., 1967.

В. И. Соболев.