Akademik

- изолированная особая точка а однозначного характера аналитич. ции f(z) комплексного переменного zтакая, что |f(z)| неограниченно возрастает при приближении к a, . В достаточно малой проколотой окрестности V= {z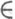С:0<|z-а|<r} точки или V'= {} в случае бесконечно удаленной точки функция f(z) представима в виде ряда Лорана специального вида:

или соответственно

с конечным числом отрицательных степеней в главной части при или соответственно конечным числом положительных степеней при . Натуральное число тв этих разложениях наз. порядком, или кратностью, полюса а; при m=1 П. наз. простым. Разложения (1) и (2) показывают, что функция р(z)=(z-a)^mf(z).при или р(z)=z^-mf(z).при аналитически продолжается в полную окрестность полюса а, причем . Иначе полюс апорядка тможно еще охарактеризовать тем, что функция 1/f(z) имеет в этой точке ануль кратности т.

Точка a=(a₁, ... , а _n) комплексного пространства 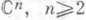, наз, П, аналитич. ции f(z) многих комплексных деременных z=(z₁, ... , z_n), если выполняются следующие условия : 1) f(z) голоморфна всюду в нек-рой окрестности Uточки а, за исключением множества P ; 2) f(z) не продолжается аналитически ни в одну точку Р;3) существует голоморфная в Uфункция такая, что голоморфная в функция р(z)=q(z)f(z).голоморфно продолжается во всю окрестность U, причем . Здесь также

однако при П., как и особые точки вообще, не могут быть изолированными.

Лит.:[1] Шабат Б. В., Введение в комплексный анализ, 2 изд., М., 1976. Е. Д. Соломенцев.