Akademik

способ определения функций от натуральных аргументов с натуральными значениями. Говорят, что (n+1)-местная функция f(x₁, ... , х _п, у). получена примитивной рекурсией из n-местной функции g( х ₁, ... , х _п).и ( п+2).местной функции h( х ₁, ... , х _n у, z), если для всех натуральных значений x₁ ... , х _п, у имеет место

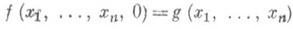
и

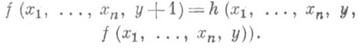
Для данных gи hтакая функция f всегде существует и единственна. При n=0 определяющие равенства для f записываются в виде

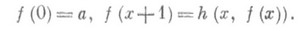
Фундаментальным свойством П. р. является то, что при любом разумном уточнении понятия вычислимости функция f, полученная из вычислимых функций gи h с помощью П. р., сама вычислимая. П. р.- одно из основных правил порождения из исходного набора простейших функций всех примитивно рекурсивных и всех частично рекурсивных функций.

Лит.:[1] Успенский В. А., Лекции о вычислимых функциях, М., 1960; [2] Мальцев А. И., Алгоритмы и рекурсивные функции, М., 1965; [3] Роджерс X., Теория рекурсивных функций и эффективная вычислимость, пер. с англ., М., 1972. С. Н. Артемов.