Akademik

генератриса, числовой или функциональной последовательности {а _п (х)} - сумма степенного ряда

с положительным радиусом сходимости. Если известна П. ф., то для изучения последовательности { а _п (х)}используются свойства коэффициентов Тейлора аналитич. ций. Для многочленов {Р _п (х)}, ортогональных на интервале ( а, b).с весовой функцией h(х), при нек-рых общих условиях существует П. ф.

Для классических ортогональных многочленов П. ф. представляется в явном виде через весовую функцию h(х).и используется для вычисления значений этих многочленов в отдельных точках, а также для вывода различных тождественных соотношений между этими многочленами и их производными.

В теории вероятностей П. ф. случайной величины x, принимающей целочисленные значения с вероятностями {Р _x (n)}, определяется формулой

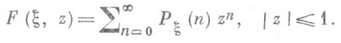
С помощью П. ф. вычисляются распределения вероятностей случайной величины x, ее математич. ожидание и дисперсия:

П. ф. случайной величины x можно определить как математич. ожидание случайной величины zx , то есть

Лит.: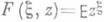.[1] Сеге Г., Ортогональные многочлены, пер. с англ.,М., 1962; [2] Суетин П. К., Классические ортогональные многочлены, 2 изд., М., 1979; [3] Феллер В., Введение в теорию вероятностей и её приложения, пер. с англ., 2 изд., т. 1-2, М., 1967. П. К. Суетин.