Akademik

- натуральное (целое положительное) число р>1, имеющее только два делителя 1 и p: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, ... Числа, имеющие не менее трех различных делителей, наз. составными. Понятие П. ч. является основным ири изучении делимости натуральных чисел. Так, основная теорема элементарной теории чисел утверждает, что всякое натуральное число, отличное от единицы, либо простое, либо, если оно составное, может быть представлено в виде произведения простых чисел. При этом такое представление единственно (с точностью до расположения сомножителей). Запись этого произведения в виде степеней одинаковых П. ч., а самих П. ч. в порядке возрастания, дает канонич. разложение натурального числа:

С помощью канонич. разложений натуральных чисел a_l, а ₂, . . ., а _k находят наибольший общий делитель d=(a₁, а ₂, . . ., a_k).и наименьшее общее кратное m=[a₁, а ₂, . . ., a_k] этих чисел. С помощью канонич. разложения натурального числа пвычисляются значения теоретико-числовых функций t(n), S(п).и j(n), к-рые обозначают соответственно число делителей, сумму делителей числа пи количество натуральных чисел , взаимно простых с п(т. е. таких, что ( т, n)=1):

Существенной особенностью этих формул является их зависимость от арифметич. структуры натурального аргумента п.

П. ч. играют роль своеобразных "кирпичиков", из к-рых строятся вес остальные натуральные числа. Еще в 3 в. до н. э. Евклид доказал бесконечность множества П. ч., а Эратосфен нашел способ отсеивания П. ч. из множества натуральных чисел (см. Эратосфена решето). Л. Эйлер (L. Euler) нашел доказательство бесконечности множества П. ч., основанное на использовании средств математич. анализа. Дальнейшее развитие аналитич. метода Эйлера оказалось очень плодотворным (см. Аналитическая теория чисел). П. Л. Чебышев открыл ряд новых законов, к-рым подчиняются П. ч. В частности, с помощью элементарных рассуждений, использующих канонич. разложение для числа n!, П. Л. Чебышев нашел неравенства, к-рым должно удовлетворять количество p(х). простых чисел :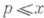

где a<1, b>1 - нек-рые положительные константы. Наиболее глубокие закономерности, к-рым подчиняется поведение последовательности П. ч., были получены путем углубления исходных идей П. Л. Чебышева с помощью аналитических и, в ряде случаев, элементарных методов (см. Распределение простых чисел).

П. ч. связаны не только с мультипликативной, но и с аддитивной структурой натуральных чисел. Достаточно характерной в этом отношении является Гольдбаха проблема о разбиении натуральных чисел на сумму трех П. ч., решенная в 1937 И. М. Виноградовым (см. Аддитивная теория чисел). Изучение законов разложения П. ч. в алгебраич. полях проливает свет на свойства обычных П. ч. Напр,, рассматривая закон разложения П. ч. в поле гауссовых чисел, получают теорему Гаусса: р=а ²+b² тогда и только тогда, когда (mod 4).

Существует много пока (1983) еще не решенных проблем, относящихся к П. ч. Напр.:

будет ли бесконечным множество П. ч. Мерсенна:

р=2^q-1, где q- простое; будет ли бесконечным множество П. ч. Ферма:

, где - целое;

существует Ли бесконечное множество П. ч. р ₁ и р ₂ "близнецов", т. е. таких, что р ₁- р ₂=2.

Экспериментальные и эвристич. соображения свидетельствуют в пользу положительного решения сформулированных выше проблем и др. аналогичных задач.

Лит.:[1] Xассе Г., Лекции по теории чисел, пер. с нем., М., 1953 Б. М. Бредихин.