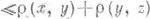 , где х, у, z - любые элементы множества X.
, где х, у, z - любые элементы множества X. Не требуется, чтобы из r( х, у)=0 следовало, что х=у. По псевдометрике r на множестве Xопределяется топология на X:точка хпринадлежит замыканию множества  , если r(x, А)=0, где
, если r(x, А)=0, где
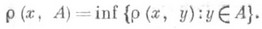
Эта топология вполне регулярна, но не обязательно хаусдорфова: одноточечные множества могут быть незамкнуты. Каждая вполне регулярная топология может быть задана семейством П. как структурное объединение отвечающих этим П. топологий. Аналогично, семейства П. могут служить для определения, описания и исследования равномерных структур.
Лит.:[1] Кепли Д ж., Общая топология, пер. с англ., 2 изд., М., 1981. А. В. Архангельский.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.