Akademik

- дифференциальное уравнение с частными производными, к-рому удовлетворяет объемный потенциал внутри областей, занятых создающими этот потенциал массами. Для ньютонова потенциала в пространстве 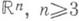, и логарифмического потенциала в П. у. имеет вид

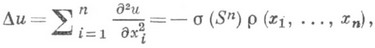
где r=r( х ₁, . . ., х _п).- плотность распределения масс, 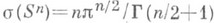- площадь единичной сферы Sⁿ в 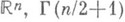- значение гамма-функции.

П. у. является основным примером неоднородного уравнения эллиптич. типа. П. у. впервые рассмотрено С. Пуассоном (S. Poisson, 1812).

Лит.:[1] Бицадзе А. В., Уравнения математической физики, М., 1976; [2] Курант Р., Уравнения с частными производными, пер. с англ., М., 1964. Е. Д. Соломенцев.