Akademik

м о д у л я - любой модуль X, содержащий данный модуль Ав качестве подмодуля. Обычно, говоря о Р. модуля А, фиксируют фактормодуль 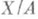, т. е. р а с ш и р е н и е м м о д у л я Ас п о м о щ ь ю м о д у л я Вназ. точную последовательность

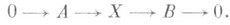
Такой модуль Xвсегда существует (напр., прямая сумма А. и В), но не определяется модулями Аи В однозначно. Как в теории модулей, так и в ее приложениях возникает потребность в обозрении всех различных Р. модуля Аспомощью В. С этой целью в классе всех Р. модуля Ас помощью Ввводится отношение эквивалентности, а на классах эквивалентных Р.- операция умножения (см. Бэра умножение), относительно к-рой множество классов эквивалентности Р. модуля Анад кольцом Rобразует абелеву группу 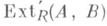. Эта конструкция обобщается и на п-к р а т н ы е Р. м од у л я Ас п о м о щ ь ю В, т. е. на точные последовательности вида

к-рым соответствует группа . Группы

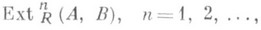
являются производными функторами функтора Ноm_R(A, В)и вычисляются с помощью проективной резольвенты модуля Аили инъективной резольвенты модуля В. Расширение Xмодуля A наз. с у щ е с тв е н н ы м, если для любого подмодуля Sмодуля Xиз =0 следует S=0. Всякий модуль обладает максимальным существенным Р., являющимся минимальным инъективным модулем, содержащим данный. Лит, см. при ст. Расширение группы. В. Е. Говоров.