д л я а л г е б р а и ч е с к и х г р у п п - утверждения о рациональности (унирациональности) или нерациональности тех или иных групповых алгебраич. многообразий. Так как абелевы многообразия всегда нерациональны, то основной интерес представляют Р. т. для линейных алгебраич. групп, Здесь проблема рациональности имеет два существенно различных аспекта: геометрический и арифметический, отвечающие соответственно алгебраически замкнутому и незамкнутому основному полю K. Первые Р. т. над полем 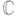 комплексных чисел были фактически доказаны еще Э. Пикаром (Е. Pi-card) и в современной терминологии устанавливают унирациональность многообразий связных комплексных групп. В явной форме проблема рациональности групповых многообразий была поставлена К. Шевалле [1] лишь в 1954. Прогресс в этом направлении тесно связан с достижениями структурной теории алгебраич. групп. Так, разложение Леви позволяет свести проблему рациональности к редуктивным группам, а разложение Брюа - доказать рациональность многообразий редуктивных групп над любым алгебраически замкнутым полем. Таким образом, в геометрич. случае имеется окончательный результат.
комплексных чисел были фактически доказаны еще Э. Пикаром (Е. Pi-card) и в современной терминологии устанавливают унирациональность многообразий связных комплексных групп. В явной форме проблема рациональности групповых многообразий была поставлена К. Шевалле [1] лишь в 1954. Прогресс в этом направлении тесно связан с достижениями структурной теории алгебраич. групп. Так, разложение Леви позволяет свести проблему рациональности к редуктивным группам, а разложение Брюа - доказать рациональность многообразий редуктивных групп над любым алгебраически замкнутым полем. Таким образом, в геометрич. случае имеется окончательный результат.
Гораздо более сложной оказывается ситуация для незамкнутых полей K. Примеры нерациональных K-многообразий доставляют уже алгебраич. торы; напр., трехмерный норменный тор 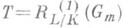 , соответствующий биквадратичному расширению
, соответствующий биквадратичному расширению 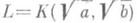 поля K(см. [1]). Этот пример минимален, ибо торы размерности
поля K(см. [1]). Этот пример минимален, ибо торы размерности 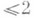 рациональны. В общем случае алгебраич. торы всегда унирациональны. Произвольные связные K-группы не обязательно унирациональны [3], однако, если поле Kсовершенно или группа G редуктивна, унирациональность имеет место (см. [1] - [4]). Тем самым проблема рациональности групповых многообразий имеет характер Люрота проблемы над незамкнутым полем.
рациональны. В общем случае алгебраич. торы всегда унирациональны. Произвольные связные K-группы не обязательно унирациональны [3], однако, если поле Kсовершенно или группа G редуктивна, унирациональность имеет место (см. [1] - [4]). Тем самым проблема рациональности групповых многообразий имеет характер Люрота проблемы над незамкнутым полем.
Так как произвольная редуктивная группа является почти прямым произведением тора и полупростой группы, то естественно различать два основных случая: 1) G- тор; 2) G - полупростая группа. В первом случае исследование проводится при помощи различных когомологич. инвариантов (для полупростых групп эти инварианты оказываются неэффективными). Достаточно законченные результаты имеются для торов, разложимых над абелевым расширением поля определения (см. [5]). Первый пример нерационального многообразия в классе полупростых групп был неодносвязной группой, конструкция к-рой фактически содержится в [10]. Возникшая при этом гипотеза о том, что многообразия односвязных групп всегда рациональны, была решена отрицательно В. П. Платоновым при помощи развитой им п р и в е д е н н о й K- т е о р и и (см. [6], [7]). Оказалось, что приведенная группа Уайтхеда SK1(D)конечномерной центральной простой K-алгебры Dтривиальна, если многообразие, определяемое SL(1, D), рационально над K. Эти результаты были перенесены на унитарные группы [12]. Ряд результатов связан с исследованием рациональности спинорных многообразий Spin (n, f), где f - невырожденная квадратичная форма над Kот ппеременных (char K№2). Спинорные многообразия рациональны, если либо  , либо поле Kявляется недискретным локально компактным или полем рациональных чисел (см. [8], [9], [11]); для
, либо поле Kявляется недискретным локально компактным или полем рациональных чисел (см. [8], [9], [11]); для  существуют нерациональные спинорные многообразия [8]. Последний результат удивителен тем, что Spin ( п, f) является двулистным накрытием рационального многообразия SO (n, f).
существуют нерациональные спинорные многообразия [8]. Последний результат удивителен тем, что Spin ( п, f) является двулистным накрытием рационального многообразия SO (n, f).
Термин "Р. т." иногда употребляется в теории алгебраич. групп в несколько ином смысле, применительно к утверждениям о свойствах групп над не обязательно алгебраически замкнутым полем. К утверждениям такого типа относится, напр., т е о р е м а Розенлихта - Гротендика о том, что любая связная K-группа обладает максимальным тором, определенным над K(с. м. [4]).
Лит.:[1] C h e v a l l e y С., "J. Math. Soc. Japan", 1954, v. 6, № 3/4, p. 303-24; [2] D e m a z u r e M., G r o t h е n d i е c k A., Schemas en groupes, B.- [u. a.], 1970; [3] R о s e n 1 i с h t M., "Ann. mat. pura appl.", 1957, v. 43, p. 25-50; [4] Б о р е л ь А., Линейные алгебраические группы, пер. с англ., М., 1972; [5] В о с к р е с е н с к и й В. Е., Алгебраические торы, М., 1977; [6] П л а т о н о в В. П., "Тр. Матем. ин-та АН СССР", 1976, т. 142, с. 198-207; [7] е г о ж е, "Докл. АН БССР", 1977, т. 21, № 3, с. 197 - 98; [8] е г о ж е, "Докл. АН СССР", 1979, т. 248, № 3, с. 524-27; [9] е г о ж е, "Тр. Матем. ин-та АН СССР", 1981, т. 157, с. 161 - 69; [10] С е р р Ж.- П., Когомологии Галуа, пер. с франц., М., 1968; [11] Ч е р н о у с о в В. И., "Докл. AН БССР", 1981, т. 25, № 4, с. 293-96; [12] Я н ч е в с к и й В. И., "Матем. сб.", 1979, т. 110, № 4, с. 579-96.
А. С. Рапинчук.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.