Akademik

ф у н к ц и й f (x) и g (x), принадлежащих ,- функция h(x), определяемая равенством

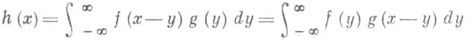
и обозначаемая символом (f*g)(x). Функция f*g определена почти всюду и также принадлежит Свертка обладает основными свойствами операции умножения, а именно:

для любых трех функций из . Поэтому с обычным сложением и умножением на число, с операцией С. в качестве умножения элементов из и с нормой

превращается в банахову алгебру (при такой норме . Если F[f] - преобразование Фурье функции f, то и это используется при решении ряда прикладных задач. Так, если задача сведена к интегральному уравнению вида

(*) где

то в предположении, что 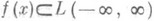, применяя к уравнению (*) преобразование Фурье, получают

откуда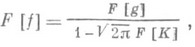

и обратное преобразование Фурье приводит к решению

уравнения (*).

Свойства С. функций находят важные приложения в теории вероятностей. Если f(x)и g(x)являются плотностями вероятности независимых случайных величин Xи Y, то С. (f*g)xесть плотность вероятности случайной величины X+Y.

Операция С. распространяется на обобщенные функции. Если fи g - обобщенные функции, из к-рых по крайней мере одна имеет компактный носитель, и j (х)принадлежит пространству основных функций, то f*g определяется равенством

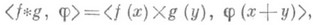
где - прямое произведение обобщенных функций f и g,т. е. функционал в пространстве основных функций двух независимых переменных такой, что

для любой финитной бесконечно дифференцируемой функции и(х, у).

С . обобщенных функций также обладает свойством коммутативности, линейности по каждому аргументу, а если по крайней мере две из трех обобщенных функций имеют компактные носители, то и свойством ассоциативности. Справедливы равенства:

где Dоператор дифференцирования и a - любой мультииндекс, , в частности , где d - дельта-функция, и если f_n, n=1, 2,. . .,- обобщенные функции такие, что и существует компакт

то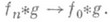

Наконец, если g - финитная обобщенная функция и f - обобщенная функция медленного роста, то к f*g применимо преобразование Фурье и снова

С. обобщенных функций широко используется при решении краевых задач для уравнений с частными производными. Так, интеграл Пуассона, написанный в виде

дает решение уравнения теплопроводности для бесконечного стержня, когда начальная температура m(х)может быть не только обычной, но и обобщенной функцией.

Понятие С. как обычных, так и обобщенных функций естественным образом переносится на случай функций многих независимых переменных: надо в предыдущем считать х, у не действительными числами, а векторами из

Лит.:[1] В л а д и м и р о в В. С., Уравнения математической физики, 4 изд., М., 1981; [2] Г е л ь ф а н д И. М., Ш и л о в Г. Е., Обобщенные функции и действия над ними, М., 1958; [3] Т и т ч м а р ш Е., Введение в теорию интегралов Фурье, пер. с англ., М.- Л., 1948. В. И. Соболев.