Akademik

- распределение вероятностей, получаемое из данного распределения перенесением массы, заключенной вне нек-рого фиксированного отрезка, на этот отрезок. Пусть вероятностное распределение на прямой задано функцией распределения F(х). Усеченным распределением, отвечающим F, наз. распределение с функцией распределения

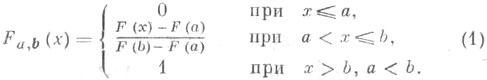
В частном случае 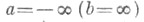У. р. наз. усеченным справа (слева).
Наряду с (1) рассматриваются У. р. вида

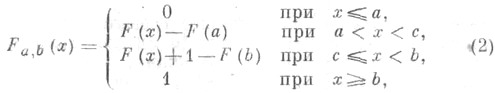
или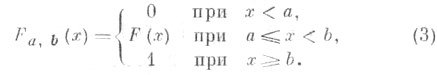

В (1) масса, сосредоточенная вне [ а, b],распределяется по всему отрезку [a, b],в (2) - помещается в точку 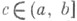(в том случае, когда а<0<b в качестве счаще всего берется точка с=0), а в (3) эта масса помещается в крайние точки аи b.
У. р. вида (1) могут интерпретироваться следующим образом. Пусть X- случайная величина с функцией распределения F(x). Тогда У. р. совпадает с условным распределением случайной величины при условии а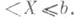
С понятием У. р. тесно связано понятие усеченной случайной величины: если X - случайная величина, то усеченной случайной величиной наз. величина

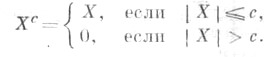
Распределение X^c является У. р. типа (3) по отношению к распределению X.
Операция усечения - переход к У. р. или усеченным случайным величинам - является весьма распространенным технич. приемом. Она позволяет, лнемного