Akademik

метод, объединяющий вариационный метод Г. М. Голузина (см. Внутренних вариаций метод).и параметрических представлений метод К. Лёвнера 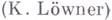для важного подкласса однолистных функций класса S, отображающих круг 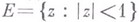на области, получающиеся из плоскости 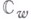проведением разрезов по кусочно непрерывным дугам. Это объединение достигается посредством специальной вариации, определяемой в простейшем случае одного жорданова разреза следующей теоремой. Пусть функция 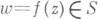отображает Ена область 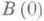, полученную из 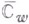проведением разреза

где 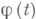непрерывна, а область 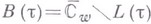, где 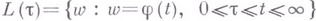, односвязна. Можно считать параметризацию разреза Lтакой, что присоединенная к 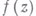функция 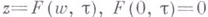, однолистно и конформно отображающая 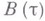на Е, нормирована условней . Пусть 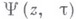обозначает функцию, обратную к 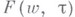при фиксированном 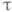. Тогда, каковы бы ни были точки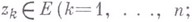 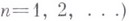и постоянные 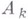, в классе S существует функция 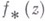, представимая в виде

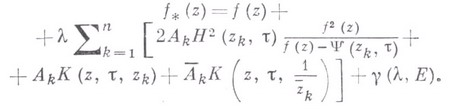
Здесь

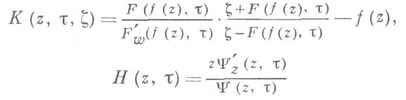
и 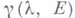- голоморфная в Ефункция, предел отношения к-рой к при равномерно стремится к иулю внутри Е.

Использование в процессе исследования экстремальных задач на классе Sспециальной (упомянутой выше) вариации и уравнения Лёвнера

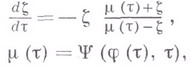
к-рому удовлетворяет функция 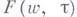при условии 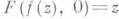, обычно позволяет получать для функции, присоединенной к экстремальной, два уравнения. Несмотря на содержащиеся в них постоянные, выражаемые через значения экстремальной функции, дальнейшее исследование этих уравнений в большом числе случаев привело к полному решению рассмотренных задач, в частности к решению задачи об области значений функционала, аналитически зависящего от функции, ее производной и сопряженных им значений на классе S. Метод был предложен П. П. Куфаревым [1] (о дальнейшем его развитии и применениях см. [2] - [5]).

Лит.:[1] Куфарев П. П., "Докл. АН СССР", 1954, т. 97, № 3, с. 391-93; [2] Александров И. А., "Уч. зап. Томск, ун-та", 1958, т. 32, с. 41-57; [3] его же, "Сиб. матем. ж.", 1963, т. 4, № 1, с. 17-31, [4] Редьков М. И., "Докл. АН СССР", 1960, т. 133, № 2, с. 284-87; [5] его же, "Изв. вузов. Математика", 1962, т. 29, с. 134-42.

И. А. Александров.