Akademik

точечная статистическая оценка, сохраняющая структуру задачи статистич. оценивания относительно заданной группы взаимно однозначных преобразований выборочного пространства.
Пусть по реализации случайного вектора X=(X₁, X₂, . . ., Х _п). компоненты к-рого X₁, X₂, . . ., Х _п суть независимые одинаково распределенные случайные величины, принимающие значения в выборочном пространстве 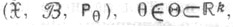надлежит оценить неизвестное истинное значение параметра 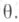Далее, пусть на действует группа взаимно однозначных преoбразований G= {g} такая, что для всех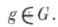
Группа Gв свою очередь порождает на параметрич. пространстве так наз. индуцированную группу преобразований 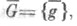элементы к-рой определяются по формуле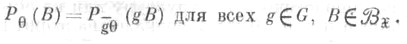

Предполагается, что является группой взаимно однозначных преобразований на таких, что для всех
В этих условиях про точечную оценку параметра говорят, что она является Э. о. или сохраняет структуру задачи статистич. оценивания параметра 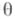относительно группы G, если

для всех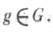
Наиболее интересные результаты в теории эквивариантной оценки получены в предположении, что функция потерь является инвариантной относительно этой же группы G.

Лит.:[1] Закс Ш., Теория статистических выводов, пер. с англ., М.. 1975; [2] Леман Э.,Проверка статистических гипотез, пер. с англ., 2 изд., М., 1979.
М. С. Никулин.