Akademik

- гладкое решение Эйлера уравнения, являющегося необходимым условием экстремума в задаче вариационного исчисления.
В случае простейшей задачи вариационного исчисления, в к-рой требуется найти экстремум функционала

среди всех кривых у(х), удовлетворяющих граничным условиям

уравнение Эйлера имеет вид

т, е. представляет собой обыкновенное дифференциальное уравнение 2-го порядка, к-рое в развернутом виде можно записать следующим образом

Если экстремум в задаче (1), (2) достигается на гладкой кривой то у(х)является Э., т. е. решением уравнения Эйлера (3) с начальным условием у(x₁)=y₁
При 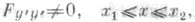уравнение Эйлерa имеет только гладкие решения (если F(x, у, у' )дважды непрерывно дифференцируемая функция). Если же F_y'y' может обращаться в нуль, то среди решений уравнения Эйлера могут быть и кусочно гладкие кривые. Пусть кусочно гладкая кривая 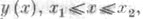доставляет экстремум в задаче (1), (2). Тогда всякий ее гладкий участок является Э., а в угловых точках (с, y(c)) должны выполняться необходимые условия Вейерштраcса - Эрдмана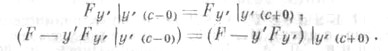

Кусочно гладкая кривая, состоящая из кусков экстремалей и удовлетворяющая в угловых точках условиям Вейерштрасса - Эрдмана, наз. ломаной Э. Если экстремум в задаче (1), (2) достигается на кусочно гладкой кривой, то эта кривая есть ломаная Э. Впрочем, часто для краткости термин лломаная