Akademik

        основанный на чётко сформулированных правилах формальный аппарат оперирования со знаниями определ. вида, позволяющий дать исчерпывающе точное описание некрого класса задач, а для некоторых подклассов этого класса — и алгоритмы решения. Примерами И. могут служить совокупность арифметич. правил оперирования с цифрами (т. е. числовыми знаками), «буквенное» И. элементарной алгебры, дифференциальное И., интегральное И. и др. ветви математич. анализа и теории функций.

        С развитием математич. логики возникла потребность в общей теории И. и в уточнении самого понятия И., которое подверглось более последоват. формализации. В большинстве случаев, однако, оказывается достаточным следующее (идущее от Гильберта) представление об И. Рассматривается некоторый алфавит, из элементов которого, именуемых буквами, с помощью чётко сформулированных правил образования строятся формулы рассматриваемого И. (наз. также иногда словами или выражениями). Некоторые из таких формул объявляются аксиомами, а из них с помощью правил преобразования (правил вывода) выводятся новые формулы, наз. теоремами данного И. Иногда термин «И.» относят лишь к словарной (выразительной) части описанного построения, говоря, что присоединение к ней дедуктивной части (т. р. добавление к алфавиту и правилам образования аксиом и правил вывода) даёт формальную систему. Если такое не интерпретированное И. сопоставить с некрой интерпретацией (т. е. дополнить чисто синститутаксич. рассмотрение некоторой семантикой), то получают формализованный язык.

        К л и н и С. К., Введение в метаматематику, пер. с англ., М., 1957, § 14—20; Карри X. В., Основания математич. логики, пер. с англ., М., 1969, гл. 2.

обладающий определенными свойствами аппарат правил оперирования со знаками, используемый при эффективном решении задач (получении искомого результата) или при доказательстве (соответственно – опровержении) предложений, выразимых с помощью этих знаков (на "языке" данного И.).

Уже с самого начала своего развития (напр., у древних египтян и вавилонян в 4–2 тысячелетиях до н.э.) математика строилась прежде всего как И. В совр. школе также начинают изучение математики с нумерации и четырех действий арифметики, т.е. с правил, относящихся к оперированию со знаками (цифрами). Лишь в Древней Греции математика впервые была построена в виде аксиоматич. теории ("Начала" Эвклида). Наряду с этой теорией продолжала, однако, существовать и арифметика, строящаяся как И. Такая арифметика называлась логистикой.

Нек-рые общие черты математических И., обусловливающие их точность и строгость и основанные на том, что математические знаки суть достаточно жесткие, легко опознаваемые (различаемые и отождествляемые) конструктивные объекты и что правила оперирования с ними также носят конструктивный (проверяемый) характер, подметил еще Лейбниц, к-рый и хотел поэтому построить логику в виде И., оперирующего, как он сам говорил, со "словами" нек-рого искусств. "языка" или, для начала, использующего "другой, менее красивый путь", к-рый "состоит в том, что, по примеру математиков, пользуются буквами, удобными для того, чтобы фиксировать наш дух, и в том, что присовокупляют доказательство в числах", т.е. пользуются арифметизированной, как говорят теперь, формой логич. И. "Я заметил, что причина того, почему мы, за пределами математики, так легко ошибаемся, между тем как геометры столь счастливы в их выводах, состоит лишь в том, что в геометрии и других частях абстрактной математики можно осуществлять поиски доказательства или проводить последовательные доказательства, сводя все к числам, – и притом не только для заключительного предложения, но и в каждый момент и на каждом шагу, который делают, исходя из посылок" (цит. по кн.: Leibniz G. W., Fragmente zur Logik, В., 1960, S. 16–17). В физике же, продолжает Лейбниц, опыт может опровергнуть заключит. результат длинной цепочки рассуждений, но не укажет, где именно в этой цепочке была ошибка. Однако идея Лейбница, полагавшего, что "единственное средство улучшить наши умозаключения состоит в том, чтобы сделать их столь же наглядными, как умозаключения математиков, так, чтобы можно было глазами найти свою ошибку и, когда возникают споры между людьми, достаточно было сказать: "Посчитаем!"..., чтобы [стало ясно, как ] увидеть, кто прав" (там же, S. 16), оказалась осуществимой полностью лишь в малоинтересных случаях И., для к-рых разрешима разрешения проблема. В этой связи интересна заметка Энгельса из подготовит. работ к "Анти-Дюрингу" (1876), в к-рой он противополагает (обычным) неточным логич. умозаключениям ("сколь многие из них оказываются ошибочными!") математич. действия, "допускающие материальное доказательство, проверку, – так как они основаны на непосредственном материальном созерцании, хотя и абстрактном", почему им и "свойственна положительная достоверность" (Маркс К. и Энгельс Ф., Соч., 2 изд., т. 20, с. 631). Уже Лейбниц подчеркивал также преимущества построения логики в виде И., обусловленные индуктивным характером последнего, – тем обстоятельством, что из небольшого числа исходных мыслей получается по порядку бесконечное множество др. мыслей. "Так из немногих чисел, взятых от единицы до десяти, могут быть выведены по порядку все остальные числа" ("Fragmente zur Logik", В., 1960, S. 24).

Однако до последнего времени термин "И." употреблялся в математике и логике без строгого общего определения. Математики создали дифференциальное и интегральное И., исчисление конечных разностей, вариационное, операционное и мн. др. И. В математич. логике были построены различные И. высказываний, И. классов, предикатов, задач, естеств. вывода, секвенций, строгой импликации, модальностей и мн. др. Потребность в общей теории И. возникла, однако, совсем недавно. В 1943 амер. ученый Э. Пост построил свою теорию "продукций", или "канонических исчислений". В 1955 в кн. "Введение в оперативную логику и математику" нем. математик и логик Лоренцен построил общую теорию И. как "оперативную логику". Развитию предложенного Лоренценом общего определения И. посвящена работа амер. логика Кёрри "Исчисления и формальные системы" (1958). Широкое общее определение дедуктивного И. в терминах алгоритмов или частично рекурсивных функций принадлежит В. А. Успенскому (1953).

Определение И. (модификация о п р е д е л е н и я Л о р е н ц е н а, см. P. Lorenzen, Einführung in die operative Logik und Mathematik, В.–Gött.–Hdlb., 1955, T. 1 – Logik): Исчисление И задается: а) алфавитом U его знаков, из к-рых будут составляться строчки, или "слова в алфавите U"; б) начальными словами И.; в) правилами, позволяющими выводить слова из уже полученных (выведенных) слов (напр., из начальных, полученного из начальных на след. шаге, и т.д.). Алфавит здесь предполагается конечным. Начальные слова И. могут задаваться как непосредственно (списком), так и с помощью "формул", т.е. слов или строчек, в к-рых, помимо букв из алфавита U, могут встречаться содержательные переменные, на место к-рых можно подставлять слова в алфавите U. Такой список или "формула" наз. "начальным правилом" и обозначается Пoi, (1 ≤ i ≤ n, где n – число начальных правил). Правила вывода также формулируются с помощью "формул", т.е. слов в алфавите U∪X представляющем собой объединение алфавита U с алфавитом X содержательных переменных (содержательных, т.е. рассматриваемых как принадлежащие к обычному языку, на к-ром мы и разговариваем об исчислении И). Эти правила имеют вид: Пk: A1(k), A2(k), ..., An(k) → A(k), (n ≥ 1)

где Пk - имя правила (k - его номер); A1^(k), ..., An^(k), A^(k) - слова (непустые) в алфавите U ∪ X; стрелка читается содержательно: как союз "если..., то" или как глагол "влечет" ("влекут"). Если в результате подстановки к.-л. слов (в т.ч. и пустых) на место содержательных переменных в "формулы" A1^(k), ..., An^(k) получаются уже выведенные (ранее) слова, то слово, полученное при этой же подстановке из "формулы" A(^k) также считается выведенным, и притом по правилу Пk. Цепочка слов, в к-рой каждое слово есть либо начальное слово, либо слово, выведенное из к.-л. предыдущих по одному из правил Пk, наз. выводом в исчислении И.

Пример И. Рассмотрим исчисление И 1, определяемое след. образом: Алфавит U состоит из букв: +, 0 (запятая здесь не является знаком алфавита). В качестве содержательной переменной для слов в этом алфавите употребляется буква X. Исчисление И 1, задается правилами: П01: 0; П1,: X → Х0; П2: X → + X +. Покажем, что в И1 выводимо слово + + 0 0 + + 0, для чего построим его вывод. [Для облегчения проверки вывода мы будем сопровождать его анализом (см. Вывод в математич. логике); на самом деле анализ здесь будет избыточной информацией: он может быть полностью восстановлен по цепочке слов вывода. Цепочка слов вывода будет при этом записываться в виде колонки, строчки к-рой последовательно занумерованы. Стрелкой указывается, из каких строчек получена данная строчка. Справа от получаемого слова помещаются имя правила, по к-рому это слово получено, и (в скобках) словá, подставляемые при этом на место содержательных переменных ].

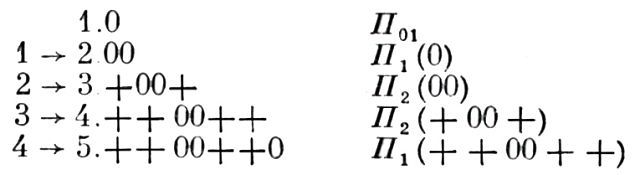Тут строчка 4, напр., содержит след. информацию о полученном в ней слове + + 0 0 + +: оно получено по правилу П2: Х → + Х +, при замене X на + 0 0 +, что дает + 0 0 + → + + 0 0 + +. Т.к. слово + 0 0 + уже выведено в строке 3, то выведено и слово + + 0 0 + +.

Основные черты И. Ясно, что для доказательства предложений, формулирующих общие свойства "слов", выводимых в И., достаточно проверить наличие этого свойства у всех начальных слов и затем убедиться в том, что правила вывода "сохраняют" это свойство, т.е., что, если слова, полученные из "формул" A1^(k), , An^(k) к.-л. (дозволенной) подстановкой на место содержательных переменных, обладают данным свойством, то и слово A^(k) тоже обладает им ("индуктивный" характер И.). Так, чтобы доказать, что все слова, выводимые в И1, содержат четное число вхождений буквы "+", достаточно заметить, что: 1) в слове "0" буква "+" вообще не содержится, т.е. число ее вхождений – четное (нуль); 2) присоединение буквы "0" справа к слову не изменяет числа вхождений буквы "+", почему, если слово X содержит четное число вхождений буквы "+", то и слово, полученное из X по правилу П1, также содержит четное число вхождений буквы "+"; 3) правило П2 также сохраняет это свойство слова X, поскольку его применение увеличивает число вхождений буквы "+" на 2, т.е. на четное число.

На вышепривед. примере можно пояснить еще одно очень существенное для всякого И. понятие допустимого правила И. Правило наз. допустимым в И., если, добавив его к правилам И., мы не увеличим запаса слов, выводимых в И., т.е., если всякий вывод, в к-ром применялось это правило, можно заменить выводом (того же слова), не содержащим применений этого правила. В нашем исчислении И1, таким правилом может быть, напр., следующее: П3: X → ++X+0+. В том, что этим правилом можно пользоваться именно потому, что без него можно обойтись, нетрудно убедиться так. Рассмотрим к.-л. вывод, где это правило применяется. В таком случае оно применяется где-то в первый раз. Пусть это будет на l-том шаге вывода, к-рый при этом будет выглядеть так:

j → 1 + + C + 0 + П3, (С),

где С – слово в алфавите {+ 0}, выведенное (в нашем примере) на j-ом шаге. Выбросим теперь из нашего вывода l-ую строку и заменим ее группой строк:

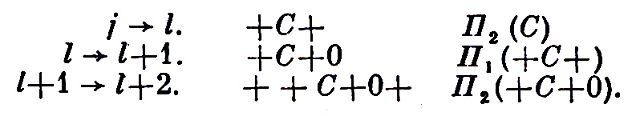Теперь слово + + С + 0 + выведено без применения правила П3, хотя, правда, вывод при этом удлинился: вместо одного применения правила П3 нам пришлось применить последовательно правила П2, П1, П2. Если в измененном т.о. выводе еще применяется где-нибудь правило П3, то опять есть строчка, где оно применяется в первый раз и где мы снова можем его применение исключить. Так мы будем поступать до тех пор, пока не исключим все применения правила П3, из нашего вывода. В более интересных случаях допустимость правила может доказываться не столь просто (напр., может потребовать индуктивного вывода). Из особенно важных теорем о допустимости нужно упомянуть прежде всего т.н. теорему о дедукции. Во мн. случаях бывает существенной, однако, возможность действительного расширения не только запаса средств И., но и запаса слов, выводимых в нем. Если "словами", выводимыми в И. (их наз. иногда "теоремами" И.), являются истинные предложения к.-л. науч. теории, то наиболее "безопасным", – в смысле невозможности сделать выводимым к.-л. ложное предложение, – является расширение И. с помощью определений, состоящих во введении новых знаков в алфавит И. и сопряженных с этими знаками правил их введения и исключения, таких, что добавление их к исчислению И не делает выводимым в расширенном исчислении И' ни одного слова в алфавите исчисления И, к-рое было невыводимым в И. (Такое расширение И., к-рое не изменяет запаса теорем, не содержащих вхождений новых знаков, наз. иногда консервативным; см., напр., Р. С. Rosenbloom, The elements of mathematical logic, N. Y., 1950, p. 164). Практически алфавит И. чаще всего бывает бесконечным. Требование конечности алфавита не налагает, однако, к.-л. существенных ограничений на определение И., поскольку в последнее всегда можно ввести правила, позволяющие и алфавит определять индуктивно, начиная с к.-л. исходных знаков; напр., так: исходный алфавит – знаки: а( ); "букву" определим индуктивно так (на место содержательной переменной X можно подставлять слова в исходном алфавите): П01: (а); П1: (Х) ( (Ха); тогда "буквами" будут слова: (а), (аа), (ааа) и т.д.; алфавит из этих букв будет уже бесконечным (о буквах, словах, алфавитах см. А. А. Марков, Теория алгорифмов, "Тр. матем. инст. им. В. А. Стеклова", [т. ] 42, М.–Л., 1954, гл. 1).

Учитывая потребности дедуктивных И., в к-рых сначала индуктивно определяются "правильно построенные" (осмысленные) формулы И., а затем задаются правила, позволяющие выделять (также индуктивно) из осмысленных формул те, к-рые являются истинными (доказанными), X. Кёрри (см. Н. Curry, Calculuses and formal systems, "Diabetica", 1958, v. 12, No 3/4) предлагает строить И. начиная с нек-рого исходного исчисления К0, определяющего объекты (слова), с к-рыми будет оперировать след. исчисление К1. Слова, выведенные в исчислении К1, в свою очередь, могут быть объектами, с к-рыми оперирует исчисление К2 и т.д. Так, напр., И. высказываний (классическое) может быть построено след. образом: сначала строим исчисление К0, алфавит к-рого состоит из знаков Р0( ). Содержательная переменная X употребляется для слов в этом алфавите. Правила исчисления К0: П01^(k0) : (р); П01(k0) : (Х) → (Хр). Теперь строим исчисление К1, алфавит к-рого состоит из знаков f ( ) ⊃ и всех слов, выводимых в К0. Содержательная переменная Ζ употребляется для слов, выводимых в К0, содержательные переменные Χ, У – для слов в алфавите исчисления К1. Правила исчисления К1: П01(k1) : Z; П1(k1) : X, Y → (X ⊃ Y). [Этим И. определяются "правильно построенные" формулы исчисления высказываний. Здесь f – знак "лжи", ⊃ – знак импликации ("если..., то"), (X ⊃ f) соответствует отрицанию формулы X. Примерами слов, выводимых в этом И., могут служить: (р), (рр), ((р) ⊃ (рр)), ((р) ⊃ f), (f ⊃ (р)). (р) ⊃ (р)). ] Исчисление К2 (определяющее "истинные" формулы И. высказываний) строится так. Его алфавит тот же, что у К1. Содержательные переменные X, У, Ζ употребляются для слов, выводимых в К1. Правила исчисления К2:

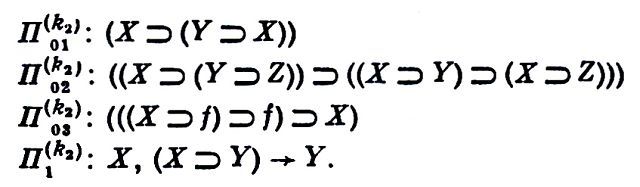[Начальные правила этого И. наз. с х е м а м и а к с и о м. Единств. правилом вывода служит modus ponens. Нетрудно показать (см., напр., А. Чёрч, Введение в математическую логику, пер. с англ., М., 1960), что из приведенных выше примеров правильно построенных формул две последние (и только эти) являются выводимыми "словами" в К2]. Такого рода сложные системы,состоящие из расположенных как бы по ступеням (или по рангам) И., – так, что переменные болеевысокого (по рангу) И. могут употребляться для слов, выводимых в И. более низкого ранга, – наз. г р а д у и р о в а н н ы м и И. Нетрудно показать, что, вводя в алфавит в качестве характеристики ступеней И. новые буквы, можно свести всякое градуированное И. к И. первой ступени.

Из определения И. ясно, что всякий вывод в И. действительно обладает той "положительной достоверностью", о к-рой шла речь в приведенной заметке Энгельса. Если отвлечься от того, что вывод может оказаться очень длинным и проверка его, по меньшей мере, утомительной, т.е. если стоять на т. зр. допустимости абстракции потенциальной осуществимости, то можно будет сказать, что всякий (законченный) вывод в И. может быть полностью проверен и для всякого слова в алфавите этого И. можно однозначно ответить на вопрос: выводится оно в д а н н о м выводе или нет. Естественно возникающим в применении ко всякому исчислению И является и вопрос о том, как по слову С в алфавите этого И. распознать, является ли оно выводимым в этом И. или нет. Этот вопрос наз. проблемой р а з р е ш е н и я для исчисления И. Но с ним ситуация уже другая. Трактуемая как задача отыскания общего метода (алгоритма), применимого к любому слову С в алфавите исчисления И и перерабатывающего его в один из ответов "да" или "нет", в зависимости от того, выводимо С в И или нет, – проблема разрешения в общем случае неразрешима. Более того, те случаи, в к-рых она разрешима, принадлежат к числу самых простых и мало интересных. В применении к логич. И. вопрос этот заведомо разрешим обычно для той ступени И., на к-рой определяются (индуктивно) правильно построенные формулы И. (нек-рая общая теорема, относящаяся к условиям его разрешимости, доказана в упомянутой статье X. Кёрри). Но уже для функциональных И. (И. предикатов) первого порядка он неразрешим на той ступени, где определяются "истинные" формулы И. (в этом и состоит содержание известной теоремы А. Чёрча; см. Алгоритм). Заметим, что проблема разрешения для исчисления И разрешима в том и только в том случае, когда можно построить такое консервативное расширение исчисления И, в к-ром, в случае выводимости слова С в И, выводимо слово ИC, а в случае невыводимости С – слово ЛC, где И (от "истина") и Л (от "ложь") – буквы, не содержащиеся в алфавите исчисления И (см. Р. С. Rosenbloom, указ. соч., р. 164, 165).

В определении И. по Лоренцену всякое правило вывода устроено так, что любой ряд слов в алфавите U исчисления И, подставляемых на место переменных, входящих в "формулы" A1^(k),, An^(k), оно перерабатывает в слово в алфавите Г, получаемое (той же подстановкой) из "формулы" А^(k), т.е. его можно трактовать как "всегда применимый" алгоритм. В определении И. по В. А. Успенскому ("Теорема Гёделя и теория алгоритмов", "Докл. АН СССР", 1953, т. 91, No 4, с. 737–40) правила вывода трактуются как алгоритмы, к-рые, будучи примененными к нек-рому ряду слов, могут и не давать ничего (не заканчиваться). Наоборот, в определении канонических исчислений по Посту (см. "Formal reductions of the general combinatorial decision problem", в журн. "Amer. journ. of math.", v. 65, No 2, 1943, p. 197–215), на "формулы" A1^(k),..., An^(k) A^(k) накладываются нек-рые дополнительные ограничения, так что на первый взгляд определение представляется более узким, чем определение Лоренцена. Тем не менее тезис, отстаиваемый Постом, состоит в том, что каждый точный язык, содержащий эффективно применимые правила вывода (т.е. без правил типа бесконечной индукции), к-рый когда бы то ни было был построен, может быть сформулирован как каноническое И. Пост ввел еще более специальное понятие н о р м а л ь н о г о И., в к-ром есть лишь одно начальное правило (аксиома), а все правила вывода ("продукции") имеют вид С1Х → ХС2 (где С1 и С2 –слова в алфавите исчисления; X – содержательная переменная), и доказал, что всякое канонич. И. имеет консервативное (Нормальное расширение (теорема Поста). В свете тезиса Поста интересно также, что Лоренцену удалось построить общую теорию И. в виде И. ("оперативной логики"), выводимыми словами к-рого являются все общедопустимые (допустимые в л ю б ы х И., их мета-исчислениях, мета-мета-исчислениях и т.д.) правила вывода, и что этим И. оказалась конструктивная, или интуиционистская, логика (исчисление Гейтинга). (He-общезначимость закона исключенного третьего в применении к понятию "выводимости в И", где И – произвольное И., явствует из того, что "не-выводимость С в И" фактически трактуется Лоренценом как выводимость слова ЛС в нек-ром консервативном расширении И' исчисления И, что сводит вопрос о применимости закона исключенного третьего к вопросу о разрешимости проблемы разрешения).

Близким к понятию И., но в нек-ром смысле более общим, является понятие формальной системы (см., напр., С. К. Клини, Введение в метаматематику, пер. с англ., М., 1957, гл. 4 и ряд соч. Кёрри, напр., Н. Curry and R. Feys, Combinatory logic, v. 1, Amst., 1958, где имеется большая библиография). Соотношению между формальными системами и И. посвящена упомянутая работа Кёрри "Исчисления и формальные системы".