Akademik

- дпнамич. характеристика поля, аналогичная импульсу в механике. Формально из ур-ний Максвелла в вакууме, связывающих векторы эл.-магн. поля E=D и Н=В (используется гауссова система единиц) с плотностями электрич. зарядов и токов j, следует соотношение:

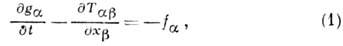
где индексы a, b=1, 2, 3 обозначают декартовы компоненты; по индексу b производится суммирование; вектор g с точностью до размерного коэф. совпадает с Пойнтинга вектором S: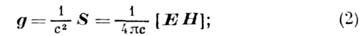

тензор Т_ab наз. Максвелла тензором натяжений: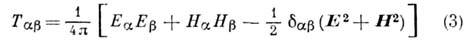

(d_ab - символ Кронекера); вектор f есть плотность силы Лоренца, действующей на объёмные электрич. заряды и токи со стороны эл.-магн. поля: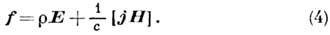

Ур-ние (1), являющееся интегралом ур-ний Максвелла, по аналогии с соответствующим соотношением в механике сплошных сред интерпретируется как закон изменения И. э. п., в к-ром вектор g, определяемый соотношением (2),- вектор плотности И. э. п. При этом тензор T_ab с обратным знаком представляет собой тензор плотности потока И. э. п., а сила Лоренца с обратным знаком является силой, действующей со стороны электрич. зарядов и токов на эл.-магн. поле. Интегрирование ур-ния (1) по произвольному объёму V даёт: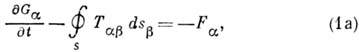

где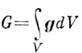

- И. э. п. в объёме V,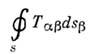

- потокa-составляющей И. э. п., втекающий внутрь объёма V через ограничивающую его поверхность s (положительной считается наружная нормаль к поверхности), F=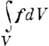- сила Лоренца, действующая на электрич. заряды и токи, находящиеся внутри объёма V. Наличие силы Лоренца в законе изменения И. э. п. (1), (1а) означает, что И. э. п. может передаваться материальнымтелам, изменяя их механич. импульс. Такой обмен импульсом может происходить, напр., в результате поглощения, излучения или рефракции эл.-магн. волн, что впервые было экспериментально подтверждено в опытах по измерению давления света (П. Н. Лебедев, 1899).С квантовой точки зрения эл.-магн. поле представляет собой ансамбль фотонов, каждый из к-рых обладает энергией 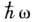и импульсом 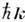, где w - частота излучения, k - волновой вектор. Обмен импульсом между полем и частицей происходит при поглощении, излучении и рассеянии фотонов заряж. частицами, напр., в Комптона эффекте. В средах, характеризующихся наличием связанных электрич. зарядов и обусловленных их движением электрич. токов, существуют два определения И. э. п. Одно из них принадлежит М. Абрагаму (М. Abraham) и совпадает с определением И. э. п. в вакууме (2). При этом для сред с линейными материальными соотношениями (D=eE, B=mH,e, m - диэлектрич. и магн. проницаемости среды) можно записать закон изменения И. э . н. типа (1), (1а), в к-ром модифицируется выражение для максвелловского тензора натяжений, а в правой части к плотности силы Лоренца, действующей на свободные электрич. заряды и токи, добавляется член: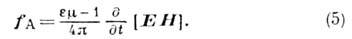

Величина f_A представляет собой плотность т. н. силы Абрагама, действующей на среду в перем. эл.-магн. поле. Структура выражения (5) такова, что плотность силы Абрагама f _А может быть включена в плотность И. з. п. При этом для плотности И. э. п. в среде получается выражение в форме Минковского (Н. Minkowski):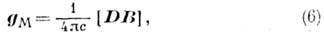

для к-рого также справедлив закон изменения И. э. п. типа (1), с модифицированным применительно к среде тензором натяжений. Формально выражение (6) для И. э. п. в форме Минковского больше соответствует духу макроскопич. электродинамики, в к-рой эл.-магн. ноле характеризуется четырьмя векторами E, D, Н. B; однако вывод закона изменения И. э. п. из yp-ний макроскопич. электродинамики также требует привлечения модели среды или материальных ур-ний в среде. Использование выражений для И. э. п. в форме Абрагама или Минковского не вызывает принципиальных противоречий, поскольку в вакууме они совпадают, а в среде с учётом разл. выражении для силы, действующей на среду в эл.-магн. поле, оба выражения удовлетворяют закону сохранения суммарного импульса среды и эл.-магн. поля. В движущихся средах, а также в любых др. средах с пространственной дисперсией И. э. п. следует отличать от импульса эл.-магн. волн, к-рый складывается из И. э. п. и импульса, обусловленного переносом энергии волновых возмущений частицами среды (пропорционального вектору Умова).В статич. эл.-магн. полях, сосредоточенных в огранич. объёме, суммарный И. э. п. всегда равен нулю, хотя поле вектора g, характеризующее распределение плотности И. э. п. в пространстве, может быть отлично от нуля. Если при этом момент И. э. п.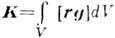

отличен от нуля, его наличие может быть экспериментально обнаружено: при включенин или выключении статич. полей система тел, поддерживающих эти поля, испытывает соответствующий момент импульса отдачи. Лит.: Тамм И. Е., Основы теории электричества, 9 изд., М., 1976; Ландау Л. Д., Лифшиц Е. М., Теория поля, 7 изд., М., 1988; их же, Электродинамика сплошных сред, 2 изд., М., 1982; Стрэттон Д. А., Теория электромагнетизма, пер. с англ., М.- Л., 1918; Гинзбург В. Л., Теоретическая физика и астрофизика, 3 изд., М., 1987. Е. В. Суворов, А. М. Фейгип.