- НАИМЕНЬШЕГО ДЕЙСТВИЯ ПРИНЦИП
-
один из вариационных принципов механики, согласно к-рому для данного класса сравниваемых друг с другом движений механич. системы действительным является то, для которого физ. величина, наз. действием, имеет наименьшее (точнее, стационарное) значение. Обычно Н. д. п. применяется в одной из двух форм.а) Н. д. п. в форме Гамильтона — Остроградского устанавливает, что среди всех кинематически возможных перемещений системы из одной конфигурации в другую (близкую к первой), совершаемых за один и тот же промежуток времени, действительным является то, для к-рого действие по Гамильтону S будет наименьшим. Матем. выражение Н. д. п. имеет в этом случае вид: dS=0, где d — символ неполной (изохронной) вариации (т. е. в отличие от полной вариации в ней время не варьируется).б) Н. д. п. в форме Мопертюи — Лагранжа устанавливает, что среди всех кинематически возможных перемещений системы из одной конфигурации в близкую к ней другую, совершаемых при сохранении одной и той же величины полной энергии системы, действительным является то, для к-рого действие по Лагранжу W будет наименьшим. Матем. выражение Н. д. п. в этом случае имеет вид DW=0, где D — символ полной вариации (в отличие от принципа Гамильтона — Остроградского, здесь варьируются не только координаты и скорости, но и время перемещения системы из одной конфигурации в другую). Н. д. п. в. этом случае справедлив только для консервативных и притом голономных систем, в то время как в первом случае Н. д. п. является более общим и, в частности, может быть распространён на неконсервативные системы. Н. д. п. пользуются для составления ур-ний движения механич. систем и для исследования общих св-в этих движений. При соответствующем обобщении понятий Н. д. п. находит приложения в механике непрерывной среды, в электродинамике, квант. механике и др.
Физический энциклопедический словарь. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1983.
- НАИМЕНЬШЕГО ДЕЙСТВИЯ ПРИНЦИП
-
- один из вариационных принципов механики, согласно к-рому для данного класса сравниваемых друг с другом движений механич. системы действительным является то, для к-рого физ. величина, наз. действием, имеет минимум (точнее, экстремум). Обычно H. д. п. применяется в одной из двух форм.
а) H. д. п. в форме Гамильтона - Остроградского. В этом случае под действием за промежуток времени t1 - t0 понимают величину
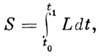
где L - ф-ция Лагранжа, зависящая от обобщённых координат системы qi, обобщённых скоростей .qi и времени t (см. Лагранжа функция).H. д. п. в этой форме устанавливает, что среди всех кинематически возможных перемещений системы из одной конфигурации в другую (близкую к первой), совершаемых за один и тот же промежуток времени t1 - t0, действительным является то, для к-рого действие S будет наименьшим. Матем. выражение H. д. п. имеет в этом случае вид

где d - символ неполной (изохронной) вариации.
б) H. д. п. в форме Мопертюи - Лагранжа. В этом случае под действием за промежуток времени t1 - t0, в течение к-рого система перемещается из конфигурации А в конфигурацию В, понимают величину
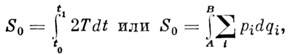
где T - кинетич. энергия системы, pi - обобщённые импульсы. H. д. п. в этой форме устанавливает, что среди всех кинематически возможных перемещений системы из конфигурации А в близкую к ней конфигурацию В, совершаемых при сохранении одной и той же величины полной энергии системы, действительным является то, для к-рого действие S0. будет наименьшим.
Матем. выражение H. д. п. в этом случае имеет вид

где D - символ полной вариации (в отличие от принципа Гамильтона - Остроградского, здесь варьируются не только координаты и скорости, но и время перемещения системы из одной конфигурации в другую). H. д. п. в форме (2) справедлив только для консервативных и притом голономных систем.H. д. п. в форме (1) является более общим и, в частности, может быть распространён на неконсервативные системы. H. д. п. пользуются для составления ур-ний движения механич. систем и для исследования общих свойств этих движений. При соответствующем обобщении понятий H. д. п. находит приложения в механике непрерывной среды, в электродинамике, квантовой механике и др.
Лит. см. при статьях Вариационные принципы механики, Действие и Динамика. С. M. Тарг.
Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.
.