Akademik

Под колебаниями атомов и ионов подразумеваются колебания массивных по сравнению с эл-нами ат. ядер. Это позволяет приписать кристаллу потенц. энергию, зависящую только от координат ядер (адиабатическое приближение).

Силы, к-рые стремятся удержать атомы в положении равновесия, приближённо можно считать пропорциональными их относит. смещениям, как если бы атомы были связаны упругими «пружинками» (рис. 1). Представление кристалла в виде совокупности ч-ц, связанных упругими силами, наз. гармоническим приближением. В такой системе могут распространяться упругие волны разной длины.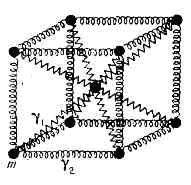

Рис. 1. Представление объёмно-центрированного кубич. кристалла в виде совокупности ч-ц массы m, связанных друг с другом «пружинками» с жёсткостью g.

При l, больших, чем межатомные расстояния (малые частоты колебаний), гармонич. приближение даёт те же результаты, что и модель кристалла как сплошной упругой среды. Для больших частот, когда длина волны сопоставима с межат. расстояниями, начинает сказываться дискр. ат. структура кристалла, при низких темп-pax проявляются квант. эффекты. Это было экспериментально обнаружено по отклонению теплоёмкости от Дюлонга и Пти закона и объяснено в теории Эйнштейна (модель кристалла как совокупности гармонич. осцилляторов, колеблющихся с одинаковой частотой) и более строго в теории Дебая, где был учтён непрерывный спектр частот осцилляторов.

Оказалось, что имеется глубокая аналогия между светом и упругими волнами в кристаллах; для последних также имеет место дискретность энергии. Кванты энергии упругих колебаний были названы фононами. Энергия фонона равна ђw (w — частота колебаний). Звук. волны в кристаллах рассматриваются как распространение квазичастиц фононов, тепловые К. к. р.— как термич. возбуждение фононов.

Можно показать, что в кристалле, состоящем из N элементарных ячеек по v атомов в каждой, существуют 3nN-6 типов простейших колебаний, наз. нормальными колебаниями или модами. Их число равно числу степеней свободы у совокупности частиц, составляющих кристалл, за вычетом трёх степеней свободы, отвечающих поступательному, и трёх — вращательному движению кристалла как целого (см. СТЕПЕНЕЙ СВОБОДЫ ЧИСЛО). Числом 6 можно пренебречь, т. к. 3vN — величина =1022— 1023 для 1 см3 кристалла. В кристалле одновременно могут существовать все возможные нормальные колебания, причём каждое протекает так, как если бы остальных не было вовсе. Любое движение атомов в кристалле, не нарушающее его микроструктуры, представляется в виде суперпозиции норм. колебаний кристалла (см. СУПЕРПОЗИЦИИ ПРИНЦИП).

Каждое норм. колебание можно представить в виде двух упругих плоских бегущих волн, распространяющихся в противоположных направлениях (н о р м а л ь н ы е в о л н ы).

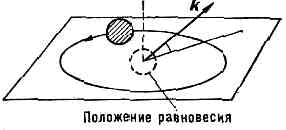Рис. 2. Эллиптич. поляризация упругих волн в кристалле; k — волн. вектор.

Плоская бегущая волна, помимо частоты w, характеризуется волн. вектором k, а также нек-рым числом s, к-рое определяет тип и поляризацию волны, т. е. направление смещения отд. атомов. В общем случае имеет место эллиптич. поляризация, когда каждый атом в данном норм. колебании описывает эллипс около своего положения равновесия (рис. 2). При этом нормаль к плоскости эллипса не совпадает по направлению с k. Эллиптич. орбиты одинаковы для идентичных атомов, занимающих эквивалентные положения в решётке. В тех кристаллах, где каждый узел явл. центром симметрии (см. СИММЕТРИЯ КРИСТАЛЛОВ), все норм. волны плоско поляризованы: атомы в любом норм. колебании совершают возвратно-поступат. движения около своих положений равновесия.

Упругие волны в кристалле всегда обладают дисперсией (см. ДИСПЕРСИЯ ВОЛН). В частности, их фазовая скорость, как правило, отличается от групповой скорости, с к-рой по кристаллу переносится энергия колебаний. Т. к. вз-ствие между атомами конечно по величине, то в кристалле существует нек-рая макс. частота колебаний wмакс (обычно wмакс=1013 Гц). Частоты норм. колебаний могут не сплошь заполнять интервал от w=0 до w=wмакс, в нём могут быть пустые участки (запрещённые зоны). Колебания, частоты к-рых соответствуют запрещённым зонам, и колебания с частотами w>wмакс не могут распространяться в кристалле. "

Акустические и оптические ветви нормальных колебаний. Все 3nN норм, колебаний объединяются в 3n групп или ветвей с разл. поляризациями по N колебаний в каждой, отличающихся значениями волн. вектора k. Для каждой ветви а (s=1, 2, 3, ... 3n) существует свой закон дисперсии w=ws(k). Если представить кристалл в виде совокупности одинаковых атомов массы т, расположенных на равных расстояниях а друг от друга и связанных попарно «пружинками» с жёсткостью g так, что они образуют бесконечную цепочку и могут смещаться только вдоль её оси (рис. 3, о), то элем. ячейка состоит из одной ч-цы и имеет только одну степень свободы.

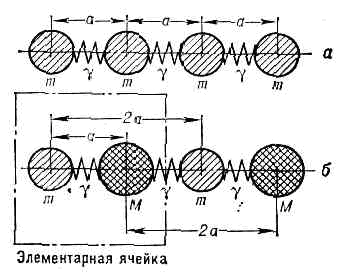Рис. 3. Простейшие модели кристалла: а — линейная одноат. цепочка; б — линейная двухат. цепочка; m и М — массы двух ч-ц, составляющих элем. ячейку.

При этом существует только одна ветвь норм. колебаний с законом дисперсии:

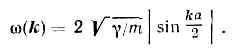У двухат. линейной цепочки (рис. 3, б) ячейка содержит две ч-цы (n=2) с массами m и М и имеются две ветви с более сложными законами дисперсии (рис. 4).

В трёхмерном кристалле всегда существуют три ветви колебаний s=1, 2, 3, наз. акустическими, у к-рых при k=0 частоты w=0. В случае, когда длина волны l значительно превышает наибольший из периодов пространств. решётки (k— мало), акустич. ветви характеризуются линейным законом дисперсии w=ck. Это обычные звук. волны (отсюда термин «акустич. ветвь»), а с — фазовая скорость их распространения, зависящая от направления распространения и поляризации. Они плоско поляризованы в одном из трёх взаимно перпендикулярных направлений, отвечающих трём значениям s=1, 2, 3 и соответствующих колебаниям кристалла как сплошной среды. В анизотропном кристалле ни одно из этих направлений обычно не совпадает с направлением распространения волны, т. е. с k. Лишь в упруго-изотропной среде звук. волны имеют чисто продольную и чисто поперечную поляризации. Акустич. ветви охватывают диапазон частот от w=0 до w=1013 Гц. С уменьшением l закон дисперсии становится более сложным.

Для остальных 3 (n-1) ветвей смещения атомов в процессе колебаний, соответствующих большой длине волны, происходят так, что центр масс отдельной элем. ячейки покоится (при k®0 атомы движутся.«навстречу» друг другу). В ионных кристаллах движение такого типа можно возбудить переменным электрич. полем, напр.

световой волной с частотой, лежащей в ИК области. Поэтому эти ветви наз. оптическими. Спектр колебаний одноат. цепочки содержит одну акустич. ветвь. В случае двухат. цепочки имеются две ветви — одна акустическая и одна оптическая (рис. 4).

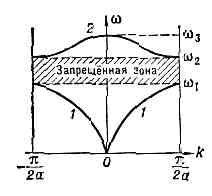Рис. 4. Закон дисперсии частот двухат. линейной цепочки: 1— акустич. ветвь; 2 — оптич. ветвь.

Ангармонизм.

В действительности межат. «пружинки» не явл. строго линейными, а колебания — строго гармоническими (ангармонизм). Нелинейность межат. «пружинок» мала (малы амплитуды колебаний), однако благодаря ей отдельные норм. колебания не независимы, а связаны друг с другом и между ними возможно вз-ствие. Ангармонизм колебаний, в частности, объясняет тепловое расширение кристаллов, отклонение теплоёмкости от закона Дюлонга и Пти в области высоких темп-р, а также отличие друг от друга изотермич. и адиабатич. упругих постоянных тв. тела и их зависимость от темп-ры и давления.

Локальные и квазилокальные колебания.

На характер К. к. р. существенно влияют дефекты крист. решётки. Жёсткость «пружинок» и массы ч-ц в области дефекта отличаются от таковых для идеального кристалла, В результате этого норм. волны не явл. плоскими. Напр., если дефект — примесный атом массы m0, связанный с соседними атомами «пружинками» с жёсткостью g0 то может случиться, что собств. частота колебаний дефекта w0=2?(g0/m0) попадёт в запрещённую область частот. В таком колебании активно участвует лишь примесный атом и его ближайшее окружение. Поэтому оно наз. локальным. Если в кристалле дефектов достаточно много, то локальное колебание, возбуждённое на одном дефекте, может перейти на другой. В этом случае локальные колебания обладают узкой полосой частот, т. е. образуют примесную зону частот К. к. р.

В области низких частот могут существовать т. н. квазилокальные колебания, в частности такие колебания имеются в кристалле с тяжёлыми примесными атомами. Квазилокальные колебания при низких темп-pax резко увеличивают решёточную теплоёмкость, коэфф. термич. расширения, тепло- и электросопротивление; напр., 2 — 3% примесных атомов, в 10 раз более тяжёлых, чем атомы осн. решётки, способны при малых темп-pax удвоить значения решёточной теплоёмкости и коэфф. термич. расширения.

Локальные колебания протяжённых дефектов, напр. дислокаций, распространяются вдоль них в виде волн, но в остальной кристалл не проникают. Частоты этих колебаний могут принадлежать как запрещённой, так и разрешённой областям частот осн. решётки, отличаясь от них законом дисперсии. Таковы, напр., звуковые поверхностные волны, возникающие у плоской границы тв. тела (в о л н ы Р э л е я).