- КОНЦЕНТРАЦИЯ НАПРЯЖЕНИЙ
-
в теории упругости и пластичности, увеличение напряжений в малых областях, примыкающих к местам с резким изменением формы поверхности тела, его сечения или с локализов. неоднородностью материала внутри тела. Факторами, обусловливающими К. н. (т. н. концентраторами напряжений или концентраторами), могут быть надрезы, выточки, выбоины, полости, усадочные раковины, трещины, инородные включения, царапины и т. п. К. н. может быть причиной разрушения тел, т. к. она снижает сопротивление тела ударным нагрузкам.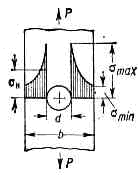 Концентрация напряжений при растяжении силой Р полосы шириной b с круглым отверстием диаметром d.При удалении от концентратора напряжения убывают быстро (рис.).Для количеств. оценки К. н. вводится понятие номинального напряжения sн— напряжения, к-рое было бы при тех же нагрузках в теле без концентратора напряжений (напр., для полосы с отверстием — равномерно распределённое норм. напряжение в той части полосы, где нет отверстия). Отношение макс. напряжения к номинальному в той же точке наз. коэфф. К. н. a=sмакс/sн, где под sмакс и sн понимаются нормальные, или касательные напряжения, или их комбинация (напр., интенсивность напряжений). Значение коэфф. К. н. зависит от формы концентратора и его абс. и относит. размеров, типа нагрузки, структуры и механич. св-в материала. К существ. перераспределению напряжений и ослаблению эффекта К. н. приводит возникновение пластич. деформации в зоне концентратора напряжений.Для уменьшения К. н. используются разгружающие надрезы, усиление зоны К. н. (напр., увеличение толщины' пластинки вокруг отверстия), технологич. приёмы упрочнения материала в зоне концентратора напряжений и т. п.Распределение напряжений при наличии концентратора напряжений определяется методами теории упругости и пластичности, а также экспериментально (тензометрированием, методом лаковых покрытий, поляризационно-оптическим методом и др.).
Концентрация напряжений при растяжении силой Р полосы шириной b с круглым отверстием диаметром d.При удалении от концентратора напряжения убывают быстро (рис.).Для количеств. оценки К. н. вводится понятие номинального напряжения sн— напряжения, к-рое было бы при тех же нагрузках в теле без концентратора напряжений (напр., для полосы с отверстием — равномерно распределённое норм. напряжение в той части полосы, где нет отверстия). Отношение макс. напряжения к номинальному в той же точке наз. коэфф. К. н. a=sмакс/sн, где под sмакс и sн понимаются нормальные, или касательные напряжения, или их комбинация (напр., интенсивность напряжений). Значение коэфф. К. н. зависит от формы концентратора и его абс. и относит. размеров, типа нагрузки, структуры и механич. св-в материала. К существ. перераспределению напряжений и ослаблению эффекта К. н. приводит возникновение пластич. деформации в зоне концентратора напряжений.Для уменьшения К. н. используются разгружающие надрезы, усиление зоны К. н. (напр., увеличение толщины' пластинки вокруг отверстия), технологич. приёмы упрочнения материала в зоне концентратора напряжений и т. п.Распределение напряжений при наличии концентратора напряжений определяется методами теории упругости и пластичности, а также экспериментально (тензометрированием, методом лаковых покрытий, поляризационно-оптическим методом и др.).
Физический энциклопедический словарь. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1983.
- КОНЦЕНТРАЦИЯ НАПРЯЖЕНИЙ
-
в теории упругости - сосредоточение больших напряжений на малых участках, прилегающих к местам с разл. рода изменением формы поверхности или сечения деформированного тела. Факторами, обусловливающими К. н. (т. н. концентраторами напряжений), являются отверстия, полости, трещины, выточки, надрезы, углы, выступы, острые края, резьба, а также разл. неровности поверхности (риски, царапины, метки, сварные швы и т. п.). Для распределения напряжений о в зоне концентрации характерно резкое изменение напряжённого состояния, сопровождаемое быстрым затуханием напряжений при удалении от этой зоны (рис. 1, а).
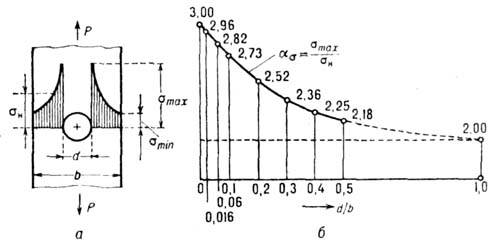
Рис. 1. Концентрация напряжений при растяжении полосы шириной b с круговым отверстием диаметра d силой P.
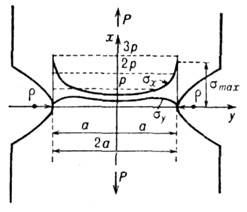
Рис. 2. Концентрация напряжений при растяжении полосы с двумя симметричными гиперболическими выточками.
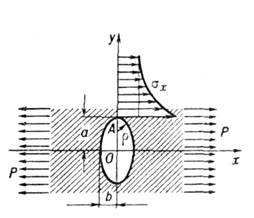
Рис. 3. Концентрация напряжений возле эллиптического отверстия в неограниченной ортотропной пластинке.
При растяжении широкого образца толщиной h с двусторонней выточкой, имеющей форму гиперболы (рис. 2), наибольшие напряжения
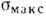 будут на контуре выточки в её вершине. Для различных
будут на контуре выточки в её вершине. Для различных 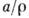 в вершине выточки
в вершине выточки
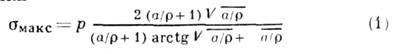
(где а-
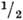 ширины образца между выточками,
ширины образца между выточками, 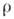 - радиус кривизны выточки,
- радиус кривизны выточки, 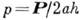 - т. н. номинальное напряжение, равное среднему нормальному растягивающему напряжению Р по наиб. узкому поперечному сечению образца). Из ф-лы (1) видно, что
- т. н. номинальное напряжение, равное среднему нормальному растягивающему напряжению Р по наиб. узкому поперечному сечению образца). Из ф-лы (1) видно, что 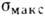 = = 2,65 р при
= = 2,65 р при 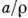 =4. По мере удаления от контура выточки s макс быстро затухают и очень скоро становятся значительно меньше р, а при уменьшении
=4. По мере удаления от контура выточки s макс быстро затухают и очень скоро становятся значительно меньше р, а при уменьшении 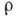 быстро возрастают. Чем больше макс. напряжение в месте концентрации по сравнению с р, тем резче наблюдается затухание напряжений при удалении от наиб. напряжённой зоны; это особенно резко проявляется в случае пространственного напряжённого состояния. Свойством быстрого затухания напряжений возле концентратора можно воспользоваться для уменьшения наиб. напряжения, имеющегося в соседстве с данным концентратором, путём устройства дополнительного нового концентратора напряжений. Этим часто пользуются для разгрузки напряжённого состояния в детали и для получения более равномерного напряжённого состояния с плавным его изменением.
быстро возрастают. Чем больше макс. напряжение в месте концентрации по сравнению с р, тем резче наблюдается затухание напряжений при удалении от наиб. напряжённой зоны; это особенно резко проявляется в случае пространственного напряжённого состояния. Свойством быстрого затухания напряжений возле концентратора можно воспользоваться для уменьшения наиб. напряжения, имеющегося в соседстве с данным концентратором, путём устройства дополнительного нового концентратора напряжений. Этим часто пользуются для разгрузки напряжённого состояния в детали и для получения более равномерного напряжённого состояния с плавным его изменением.
Количественной оценкой К. н. служат коэф. К. н.
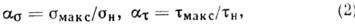 i
i
где
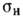 и
и 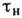 - номинальные напряжения. На рис. 1 ( б )приведены
- номинальные напряжения. На рис. 1 ( б )приведены 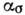 в плоском образце с круговым отверстием для разл. отношений d/b.
в плоском образце с круговым отверстием для разл. отношений d/b.
Анизотропия упругих свойств материала оказывает сильное влияние на величину
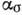 лишь в небольшой области вблизи концентратора, а по мере удаления от концентратора напряжений
лишь в небольшой области вблизи концентратора, а по мере удаления от концентратора напряжений 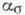 быстро затухает, как и в случае изотропной среды. Так, напр.,
быстро затухает, как и в случае изотропной среды. Так, напр., 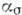 в точке А (рис. 3) эллиптич. отверстия, находящегося в неогранич. ортотропной пластинке, характеризуемой упругими константами
в точке А (рис. 3) эллиптич. отверстия, находящегося в неогранич. ортотропной пластинке, характеризуемой упругими константами 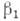 и
и 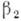 , определяется по ф-ле
, определяется по ф-ле
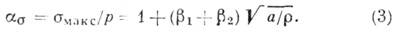
Для изотропной среды
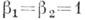 и
и

Из (3) и (4) следует, что в случае малых отверстий номинальным напряжением
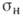 будут напряжения р в соответствующей точке неослабленной пластинки, находящейся под действием той же системы внеш. усилий, что и ослабленная данным отверстием пластинка.
будут напряжения р в соответствующей точке неослабленной пластинки, находящейся под действием той же системы внеш. усилий, что и ослабленная данным отверстием пластинка.
Различают теоретический коэф. К. н., определяемый методами классич. теории упругости [ф-лы (1), (3)], и техн. коэф. К. н., учитывающий структуру и пластич. свойства материала. Коэф. К. н. зависит гл. обр. от радиуса кривизны поверхности концентратора в окрестности точки с наиб. напряжением; при неогранич. уменьшении радиуса кривизны теоретич. коэф. К. н. неограниченно возрастает, что не подтверждается экспериментально. Поэтому при малых r величина as условная, т. к. в зоне К. н. перемещения не являются малыми, и при сравнимых с величиной кристалла (для кристаллич. материалов) теряет силу основное допущение теории упругости - гипотеза идеальной сплошности среды. Эксперименты по определению предела выносливости образцов с выточками показывают, что существует предельное значение р для выточек, после уменьшения к-рого не наблюдается уменьшения предела выносливости образца. Так, для мягкой стали таким радиусом будет
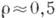 мм, для алюминия
мм, для алюминия 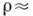 0,1-0,15 мм. Техн. коэф. К. н. определяется экспериментально и всегда остаётся ограниченным.
0,1-0,15 мм. Техн. коэф. К. н. определяется экспериментально и всегда остаётся ограниченным.
К. н. часто является причиной возникновения и развития усталостных трещин, а также статич. разрушения деталей из хрупких материалов. Внесение концентратора напряжений вызывает также снижение предела усталости образца и смещение кривой усталости. Отношение предела усталости образца без К. н. (
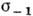 или
или 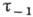 ) к пределу усталости образца с К. н. (
) к пределу усталости образца с К. н. (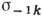 или
или 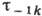 ), имеющего такие же абсолютные размеры сечений, как и первый, наз. эффективным коэф. К. н. (
), имеющего такие же абсолютные размеры сечений, как и первый, наз. эффективным коэф. К. н. (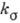 или
или 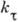 ):
): 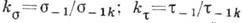 . Коэф.
. Коэф. 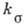 и
и 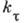 обычно меньше, чем теоретич. коэф.
обычно меньше, чем теоретич. коэф. 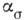 и
и 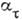 Для количественной оценки этой разницы вводятся коэффициенты чувствительности материала к К. н.:
Для количественной оценки этой разницы вводятся коэффициенты чувствительности материала к К. н.: 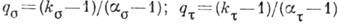 Чувствительность детали к К. н. зависит прежде всего от свойств материала, из к-рого она изготовлена.
Чувствительность детали к К. н. зависит прежде всего от свойств материала, из к-рого она изготовлена.
Большинство решений о распределении напряжений в местах концентрации относится к плоским задачам теории упругости и пластичности или получено на основе упрощающих гипотез теории пластин и оболочек. Поэтому К. н. изучается в основном экспериментально (методом фотоупругости, тензометрирования и др.). В последние годы исследован ряд пространственных задач К. н. методом "замораживания" деформаций (см. Поляризационно-оптический метод). Для уменьшения или устранения К. н. применяются разгружающие надрезы, усиления края отверстий и вырезов рёбрами жёсткости, накладками и др., а также упрочнение материала в зоне К. н. разл. способами технол. обработки.
Лит.: Нейбер Г., Концентрация напряжений, пер. с нем., М.- Л., 1947; Савин Г. Н., Распределение напряжений около отверстий, К., 1968; Серенсен С. В., Сопротивление материалов усталостному и хрупкому разрушению, М., 1975; Методы расчета оболочек, т. 1 - Теория тонких оболочек, ослабленных отверстиями, К., 1980.
Г. Н. Савин, В. И. Савченко.
Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.
.