- ПЛОСКАЯ ВОЛНА
-
волна, у к-рой направление распространения одинаково во всех точках пространства. Простейший пример — однородная монохроматич. незатухающая П. в.:и(z, t)=Aeiwt±ikz, (1)где А — амплитуда, j= wt±kz — фаза, w=2p/Т — круговая частота, Т -период колебаний, k — волновое число. Поверхности постоянной фазы (фазовые фронты) j=const П. в. являются плоскостями.При отсутствии дисперсии, когда фазовая скорость vф и групповая скорость vгр одинаковы и постоянны (vгр=vф= v), существуют стационарные (т. е. перемещающиеся как целое) бегущие П. в., к-рые допускают общее представление вида:u(z, t)=f(z±vt), (2)где f — произвольная функция. В нелинейных средах с дисперсией также возможны стационарные бегущие П. в. типа (2), но их форма уже не произвольна, а зависит как от параметров системы, так и от характера движения волны. В поглощающих (диссипативных) средах П. в. уменьшают свою амплитуду по мере распространения; при линейном затухании это может быть учтено путём замены в (1) k на комплексное волновое число kд ± ikм, где kм — коэфф. затухания П. в.Однородная П. в., занимающая всё бесконечное пространство, является идеализацией, однако любое волновое поле, сосредоточенное в конечной области (напр., направляемое линиями передачи или волноводами), можно представить как суперпозицию П. в. с тем или иным пространств. спектром k. При этом волна может по-прежнему иметь плоский фазовый фронт, но неоднородное распределение амплитуды. Такие П. в. наз. плоскими неоднородными волнами. Отдельные участки сферич. и цилиндрич. волн, малые по сравнению с радиусом кривизны фазового фронта, приближённо ведут себя как П. в.
Физический энциклопедический словарь. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1983.
- ПЛОСКАЯ ВОЛНА
-
- волна, ук-рой направление распространения одинаково во всех точках пространства. Простейший пример - однородная монохроматич. незатухающая П. в.:
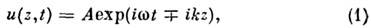
где А - амплитуда,
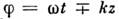 - фаза,
- фаза,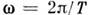 - круговая частота, Т - период колебаний, k - волновое число. Поверхности постоянной фазы (фазовые фронты)
- круговая частота, Т - период колебаний, k - волновое число. Поверхности постоянной фазы (фазовые фронты)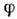 = const П. в. являются плоскостями.
= const П. в. являются плоскостями.
При отсутствии дисперсии, когда фазоваяскорость v ф и групповая скорость v гр одинаковы и постоянны (v гр = v ф= v) существуют стационарные (т. е. перемещающиеся как целое) бегущиеП. в., к-рые можно представить в общем виде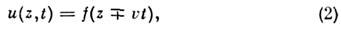
где f - произвольная ф-ция. В нелинейныхсредах с дисперсией также возможны стационарные бегущие П. в. типа (2),но их форма уже не произвольна, а зависит как от параметров системы, таки от характера движения волны. В поглощающих (диссипативных) средах П. в. уменьшают свою амплитуду по мере распространения; при линейном затуханииэто может быть учтено путём замены в (1) k на комплексное волновоечисло k д
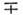 ik м,где k м - коэф. затухания П. в. Однородная П. в., занимающаявсё бесконечное пространство, является идеализацией, однако любое волновоеполе, сосредоточенное в конечной области (напр., направляемое линиямипередачи или волноводами), можно представить как суперпозициюП. в. с тем или иным пространственным спектром k. При этом волнаможет no-прежнему иметь плоский фазовый фронт, во неоднородное распределениеамплитуды. Такие П. в. наз. плоскими неоднородными волнами. Отд. участкисферич. или цилиндрич. волн, малые по сравнению с радиусом кривизны фазовогофронта, приближённо ведут себя как П. в.
ik м,где k м - коэф. затухания П. в. Однородная П. в., занимающаявсё бесконечное пространство, является идеализацией, однако любое волновоеполе, сосредоточенное в конечной области (напр., направляемое линиямипередачи или волноводами), можно представить как суперпозициюП. в. с тем или иным пространственным спектром k. При этом волнаможет no-прежнему иметь плоский фазовый фронт, во неоднородное распределениеамплитуды. Такие П. в. наз. плоскими неоднородными волнами. Отд. участкисферич. или цилиндрич. волн, малые по сравнению с радиусом кривизны фазовогофронта, приближённо ведут себя как П. в.Лит. см. при ст. Волны.
М. А. Миллер, Л. А. Островский.
Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.
.