Akademik

ПЬЕЗОЭЛЕКТРИКИ

ПЬЕЗОЭЛЕКТРИКИ: кристаллические вещества, в к-рых при сжатии или растяжении в определённых направлениях возникает электрич. поляризация даже в отсутствии электрич. поля (п р я м о й п ь е з о э ф ф е к т). Следствием прямого пьезоэффекта явл. о б р а т н ы й п ь е з о э ф ф е к т — появление механич. деформации под действием электрич. поля. Связь между механич. и электрич. переменными (деформацией и электрич. полем) носит в обоих случаях линейный характер. Обратный пьезоэффект следует отличать от электрострикции. Первое подробное исследование пьезоэффектов было проведено в 1880 франц. физиками братьями Ж. и П. Кюри на кристалле кварца. В дальнейшем пьезоэлектрич. св-ва были обнаружены более чем у 1500 в-в (см. ПЬЕЗОЭЛЕКТРИЧЕСКИЕ МАТЕРИАЛЫ).

Чтобы обнаружить пьезоэффект, на грани крист. пластинки накладывают металлич. обкладки. Если обкладки разомкнуты, то при деформациях пластинки между ними возникает разность потенциалов. В случае замкнутых обкладок на них при деформации появляются заряды, равные по величине (но противоположные по знаку) поляризац. зарядам, возникающим на поверхностях пластинки, и в цепи, соединяющей обкладки, течёт ток. При подключении к обкладкам внешней эдс кристалл деформируется.

Механизм пьезоэффекта можно пояснить на примере кристалла кварца (рис. 1), элем. ячейка к-рого, содержащая три молекулы SiO2, схематически изображена на рис. 2. При сжатии вдоль оси Х1 положит. ион 1(Si+) и отрицат. ион 2(O-) перемещаются в глубь ячейки, в результате чего на плоскостях А и В появляются заряды. При растяжении на плоскостях А и В возникают заряды противоположного знака. Пьезоэффекты наблюдаются только в кристаллах, не имеющих центра симметрии. Справедливо общее утверждение: в кристаллах, обладающих центром симметрии, пьезоэффект невозможен. Наличие др. элементов симметрии (оси, плоскости симметрии; (см. СИММЕТРИЯ КРИСТАЛЛОВ) может запрещать появление поляризации в некоторых направлениях или при деформациях, т. е. также ограничивает число кристаллов — П. В результате П. могут принадлежать лишь к 20 точечным группам симметрии (из 32): 1, 2, 3, 4, 6, т, mm2, 3m, 4mm, 6mm, 222,4, 422, 42m, 6, 622, 6m 2, 32, 23m, 3. Кристаллы первых 10 классов — пироэлектрики, т. е. обладают поляризацией в отсутствие внешних воздействий. В этих кристаллах пьезоэффект проявляется, в частности, в изменении величины спонтанной поляризации при механич. деформации. Пьезоэлектрич. св-ва можно создавать в некоторых некристаллических диэлектриках за счёт образования в них т. н. пьезоэлектрической текстуры, напр. поляризацией в электрическом поле (пьезокерамика), механич. обработкой (древесина) и др.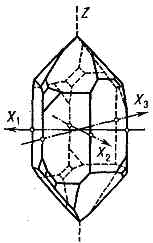

Рис. 1. Кристалл кварца SiO2.

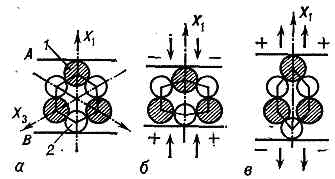Рис. 2. Схема структуры кварца: проекции ионов Si+ и О- на плоскость, перпендикулярную оси третьего порядка. Заштрихованные кружки Соответствуют ионам Si+, светлые — паре ионов О-; а, — недеформированное состояние; б — сжатие вдоль оси X1; в — растяжение вдоль оси X1.

Количеств. хар-кой пьезоэффекта явл. совокупность пьезоконстант — коэфф. пропорциональности в соотношениях между электрич. величинами (напряжённость электрич. поля Е, поляризация P) и механич. величинами (механич. напряжения s, относит. деформации u). Напр., поляризация, возникающая в П. под действием механич. напряжения s, выражается соотношением P=ds. Полная поляризация (с учётом электрич. поля) складывается из поляризации, вызванной механич. напряжением, и поляризации, вызванной электрич. полем. Она равна: P=ds+cE(c диэлектрич. восприимчивость). Коэфф. d — одна из пьезоконстант. Т. к. механич. напряжения могут быть представлены как совокупность шести независимых величин (сжатия и растяжения вдоль трёх осей, а также сдвиги в плоскостях, перпендикулярных этим осям), а вектор поляризации имеет три независимые компоненты, то в общем случае может быть 18 разных пьезоконстант. Пьезоконстантами наз. также коэфф. в соотношениях: P=ru+cЕ, u=ss+gP (коэфф. s — упругая податливость) и т. п. Все пьезоконстанты (d, r, g) связаны друг с другом, так что при описании пьезоэлектрич. св-в кристалла можно ограничиться только константами одного типа, напр. d.

Величины пьезоконстант сильно различаются для кристаллов разных типов. Для ионных кристаллов порядок величины пьезоконстант можно оценить след. образом. Допустим, что разноимённые ионы сдвинулись под действием механич. напряжения s на расстояние l. Возникший при этом дипольный момент на единицу объёма P=е1/а3, где е — заряд иона (можно считать равным заряду эл-на), а — постоянная решётки. Относит. деформация u=l/а. Из выражений P=ds и s=cu (Гука закон) следует, что d=P/s=P/lcu=e/a2c. Принимая е= =10-10 ед. СГСЭ, a=10-8—10-7 см, а с=1012 СГСЭ, получим d=10-6— 10-8 ед. СГСЭ. Для кварца, напр., величины пьезоконстант составляют неск. ед. на 10-8 ед. СГСЭ. Существенно больших величин могут достигать пьезоконстанты у сегнетоэлектриков, т. к. их поляризация может быть связана с перестройкой доменной структуры при механич. деформации.

П. применяются в технике и лабораторной практике, медицине и др.

ПЬЕЗОЭЛЕКТРИКИ

- вещества, в к-рых при определённых упругих деформациях (напряжениях) возникает электрич. поляризация даже в отсутствие элек-трич. поля (прямой пьезоэффект). Следствием прямого пьезоэффекта является обратный пьезоэффект - появление механич. деформаций под действием электрич. поля. Проявления прямого и обратного пьезоэффектов могут быть различными, первый может выражаться, напр., в появлении при деформации электрич. поля в отсутствие поляризации, второй - в возникновении при наложении электрич. поля упругих напряжений в отсутствие деформаций. В общем виде речь идёт о линейной связи между механич. и электрич. переменными (первые -деформация и, напряжение s; вторые - поляризация Р, электрич. поле Е, электрич. индукция D; см. Диэлектрики), Первое подробное исследование пьезоэффектов проведено Ж. и П. Кюри (J. et P. Curie) (1880) на кристалле кварца. В дальнейшем пьезоэлектрич. свойства были обнаружены более чем у 1500 веществ.


	Полупроводник
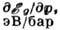
	Si	5,2
	Ge	13
	GaSb	14,7
	GaAs	11
	InSb	15,5
	InAs	10
	ZnS, ZnSe	6
	CdS	4,9
	CdSe	6
	GaS	- 2
	GaSe	- 5
	InSe	- 3,5

Пьезоэффекты наблюдаются только в кристаллах, не имеющих центра симметрии. (В кристаллах, обладающих центром симметрии, пьезоэффект невозможен.) Наличие др. элементов симметрии (оси, плоскости симметрии; см. Симметрия кристаллов )может запрещать появление поляризации в нек-рых направлениях или при деформациях, т. е. также ограничивает число кристаллов - П. В результате П. могут принадлежать лишь к 20 точечным группам симметрии (из 32) : 1,2,3, 4, 6, m, mm2, 3m, 4mm, 6 тт,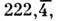422,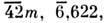

6m2, 32, 23, т3. Кристаллы первых 10 классов - пироэлектрики, т. е. обладают поляризацией в отсутствие внеш. воздействий. В этих кристаллах пьезоэффект проявляется, в частности, в изменении величины спонтанной поляризации при механич. деформации. Пьезоэлектрич. свойства можно создавать в нек-рых некристаллич. диэлектриках за счёт образования в них т. н. пьезоэлектрич. текстуры, напр. поляризацией в электрич. поле (пьезокерамика), механич. обработкой (древесина) и др. (см. Пьезоэлектрические материалы).

Количеств. характеристикой пьезоэффектов в кристалле является совокупность пьезоконстант (пьезомодулей) - коэф. пропорциональности между электрич. и механич. величинами. При этом одна электрич. величина (напр., Р )зависит как от др. электрич. величины (напр., Е), так и от механич. величины ( и или s). Напр.: поляризация, возникающая в П. под действием деформации (s) 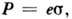где е- пьезомодуль. Полная поляризация с учётом электрич. поля Е выражается соотношением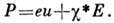

Величина 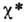имеет смысл диэлектрической восприимчивости при постоянной деформации. Т. к. механич. деформации могут быть представлены как совокупность 6 независимых величин (сжатия и растяжения вдоль 3 осей. а также сдвигов в плоскостях, перпендикулярных осям), а вектор поляризации P имеет 3 компоненты, то в наим. симметричных кристаллах может быть 18 разных пьезоконстант.

Симметрия кристалла ограничивает число независимых пьезомодулей, напр. кристалл точечной группы симметрии 422 имеет только одну независимую пьезо-константу. Пьезоконстантами являются также величины d, а, b,l, s в соотношениях

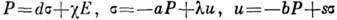
и т. п. Все пьезоконстанты связаны друг с другом, так что при описании пьезоэлектрич. свойств можно ограничиться только одной совокупностью констант, напр. е.

Величины пьезоконстант различаются для кристаллов разных типов. Для ионных кристаллов порядок величины пьезоконстант можно оценить след. образом: пусть при деформации закороченного кристалла ( Е = 0) изменение постоянной решётки (l )равно DZ, так что деформация Разноимённые ионы сдвигаются друг относительно друга на величину ~Dl, а поляризация 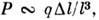где q- заряд иона

(можно считать равным заряду электрона). Т. о., порядок пьезоэлектрич. константы такой же, как и у атомного электрич. поля 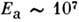единиц СГСЭ. Существенно больших величин могут достигать пьезоконстанты у сегнетоэлектриков, т. к. их поляризация может быть связана с перестройкой доменной структуры при механич. деформации.

Наличие пьезоэффектов сказывается на характере разл. акустич. явлений. Так, одна из объёмных упру гих волн становится поверхностной (Гуляева - Блюштейна волна). Отражение и пропускание упругой волны на границе П. и др. среды могут определяться не только соотношением модулей упругости сред, но и тем, является ли др. среда диэлектриком или проводником. Коэф. усиления звука за счёт дрейфа носителей заряда в полупроводнике имеет разную зависимость от частоты звука в П. и в центросимметричных кристаллах.

П. используются в технике в качестве преобразователей механич. колебаний в электрические и электрических - в механические. Они являются осн. материалами акустоэлектропики.

Лит.: Ландау Л. Д., Лифшиц E. М., Электродинамика сплошных сред, 2 изд., М., 1982; H аи Дж., Физические свойства кристаллов и их описание при помощи тензоров и матриц, пер. с англ., 2 изд., М., 1967; Сиротин Ю. И., Шаскольская М. П., Основы кристаллофизики, 2 изд., М., 1979; Таганцев А. К., Пиро-, пьезо-, флексоэлектрический и термополяризационный эффекты в ионных кристаллах, "УФН", 1987, т. 152, в. 3, с. 423.

А. П. Леванюк, Д. Г. Санников.

Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.