Akademik

СОПРОТИВЛЕНИЕ ИЗЛУЧЕНИЯ

СОПРОТИВЛЕНИЕ ИЗЛУЧЕНИЯ: активное сопротивление RS, характеризующее излучат. способность антенны. Полная мощность излучения интерпретируется при этом как мощность, поглощаемая в RS. Любой фидерный тракт, по к-рому эл.-магн. энергия поступает к антенне (двухпроводная линия, волновод и др.), можно считать нагруженным на входное сопротивление антенны, складывающееся из сопротивления джоулевых потерь и импеданса излучения, активная часть к-рого равна RS. С. и. зависит от формы, размеров, материала антенны, распределения токов в ней, диэлектрич. e и магн. m проницаемостей окружающей среды и от св-в пространства, в к-рое происходит излучение (неограниченное пространство, свободное от искажающих поле объектов; пространство, ограниченное проводящей границей, излучение внутрь др. волновода или объёмного резонатора и т. п.). В свободном пространстве вибратор Герца имеет

RS=(1/6p)?(m/e)(kl)2 Ом (k — волновое число, l — длина волны вибратора, l-l), что для вакуума (e=m=1) даёт: RS=8p2(l/l)2 Ом. Соответственно полуволновой вибратор в вакууме имеет RS=73,1 Ом. Проволочная рамка площадью а с током обладает при s-l С. и. RS=(1/6p)?(m/e)(k2s)2 Ом, т. е: в вакууме: .RS=320p2(s/l2)2 Ом.

СОПРОТИВЛЕНИЕ ИЗЛУЧЕНИЯ: - активное сопротивление антенны илилюбого др. излучателя, потери мощности в к-ром эквивалентны её уносу волнамив окружающее пространство, т. е. излучению. Обычно С. и. вводят как составляющуювходного сопротивления антенны Z_BX при подключении последнейк линии передачи с волновым сопротивлением Z_B. Для простейшейэквивалентной схемы последовательно соединённых сопротивлений 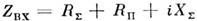, где 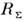-С. и., R_П - сопротивление омических потерь,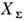- реактивное сопротивление, обусловленное полями в реактивных элементахантенны (ёмкостях и индуктивностях), а также в полях стоячих волн, сосредоточенныхв её окрестности (иногда эту часть реактивного сопротивления называют реактансомизлучения). Идеальное согласование идеального излучателя (R_П= 0) с идеальной линией 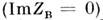достигается при выполнении условий 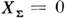,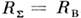. М. А. Миллер.