Akademik

(от франц. echelette-лесенка, лестница) - оп-тич. элемент, плоская отражат. фазовая дифракционная решётка с треугольной формой штрихов. Используется как диспергирующий элемент в дифракц. спектральных приборах для разложения оптич. излучения в спектр. Э. изготовляется нарезанием на плоской металлич. поверхности (с помощью спец. делительной машины с алмазным резцом) строго параллельных штрихов, необходимая треугольная форма к-рых (рис. 1) определяется формой режущей грани резца. Э. изготовляются также спец. методами, такими, как полимерные копии- реплики с нарезных Э., покрытые тонким слоем металла. Голографич. методы изготовления дифракц. решёток не позволяют изготовлять Э. со строго треугольной несимметричной формой штрихов, а лишь с приближённой к ней формой и лишь для УФ-, видимой и ближней ИК-областей.

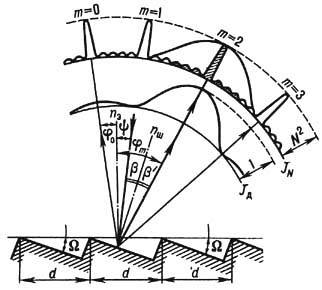
Рис. 1. Схематическое изображение функций J_N , J _д и их произведения J _дJ_N=1N² (заштриховано): направления j_m на центр дифракционного максимума функции J _д совпа дает с интерференционным максимумом функции J_N при т =2; п _э- нормаль к плоскости эшелетта, п _ш- нормаль к грани штриха.

Формулы для расчёта спектроскопич. характеристик Э., такие как осн. соотношение - т. н. формула дифракц. решётки d(siny + sinj) = ml, выражения для угл. дисперсии dj/dl, разрешающей силы R =l/dl, области дисперсии Dl =l₁/m (d- период решётки, y- угол падения, j- угол дифракции, т - порядок спектра, dl - минимально разрешаемый спектральный интервал длин волн, l₁ - коротковолновая граница спектра исследуемого излучения), такие же, как и для амплитудной (напр., щелевой) дифракц. решётки, т. к. они связаны с периодич. структурой решётки и не зависят от формы штриха. Осн. отличие и существ. практич. преимущество Э. перед амплитудной дифракц. решёткой состоит в том, что у Э. при определ. схеме установки один из образуемых им спектров ненулевого порядка (m0) может иметь наиб. интенсивность по сравнению с остальными спектрами др. порядков. В этот спектр ненулевого порядка Э. концентрирует большую часть падающего на него потока энергии (до 80%), что позволяет создавать дифракц. спектральные приборы высокой светосилы.

Расчёт результирующего распределения интенсивности в плоскости дисперсии спектр. прибора с Э. (в плоскости, перпендикулярной штрихам Э.), проведённый на основе Гюйгенса - Френеля принципа, показывает, что оно пропорционально произведению двух ф-ций - интерференционной J_N и дифракционной J _д: J _рез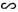J_NJ _д. Интерференц. ф-ция J_N = (sinNq/sinq)² - результат интерференции когерентных пучков, дифрагированных от всех N штрихов Э. [здесь q = (p/l)d(siny+sinj)]. Она имеет вид эквидистантных резких максимумов разл. порядков т и одинаковой пиковой интенсивности, пропорциональной N² при 0 = mp, откуда следует: d(siny + sinj)= ml. Дифракц. ф-ция J _д = (sin и/и)² - результат дифракции на отд. штрихах Э.; здесь u = (p/l)d[(sin y+ sin j) - tgW(cosy + cosj)]. В отличие от J_N ф-ция J _д зависит от формы штриха Э.- угла W "скоса" пологой грани несимметричного треугольного штриха (рис. 1). Макс. значение ф-ции J _д=1при u = 0; по обе стороны от максимума она относительно быстро уменьшается (как при дифракции на щели, см. Дифракция света).

Макс. значение произведения этих ф-ций (J_N)_mах(J _д)_mах = = N²•1, а следовательно, и макс. интенсивность спектра будет в том случае, если интерференц. максимум ф-ции J_N к.-л. порядка т0 совпадает с центром дифракц. максимума ф-ции J _д. Для этого необходимо, чтобы направление j_mах в ур-нии d(siny + sinj_mах) = ml, совпало с направлением j _{д mах} на центр максимума ф-ции J _д. Ф-ция J _д = (sin и/и)². при и =0равна 1, тогда для выполнения указанного условия углы j_mах и y, входящие в ур-ние решётки, должны одновременно удовлетворять соотношению

В случае Э. это возможно, т. к. положение максимумов ф-ции J_N (при заданных y и d )не зависит от формы штриха (угла W) и, изменяя величину W, можно совместить направление на центр ф-ции J _д с любым максимумом ф-ции J_N порядка т0. В этом и состоит осн. преимущество Э. перед амплитудной решёткой, у к-рой максимум ф-ции J _д совпадает с максимумом ф-ции J_N нулевого порядка ( т =0), к-рый является ахроматическим, т. е. не образует спектра. На рис. 1 схематически изображены ф-ции J_N и J _д и их произведение (штриховка). Здесь дифракц. максимум J _д точно совпадает с интерференц. максимумом 2-го порядка.

Соотношение (1) имеет простой геом. смысл. Если на Э. падает луч (здесь и далее слово "луч" означает параллельный пучок), образующий угол с нормалью п _э к плоскости

Э., то направление j_m на центр ф-ции J _д определяется по закону зеркального отражения от рабочей пологой грани штриха, т. е. углы b и b' (рис. 1), образованные падающим и дифрагированным j_mах лучами с нормалью п _ш. к грани штриха, равны: b' = b. Угол j_mах, удовлетворяющий условию (1), наз. углом "блеска" (blaze), а длину волны, для к-рой выполняются это условие и условие d(siny + sinj_max) = =ml _бл,- длиной волны "блеска" l _бл. Область длин волн вблизи l _бл наз. областью высокой концентрации энергии в данном порядке спектра, здесь образуется спектр наиб. интенсивности. Однако выполнение условий "блеска" приводит к искажению интенсивности линий регистрируемого спектра. Если, напр., в исследуемом спектре имеется неск. спектральных линий одинаковой интенсивности, то в образовавшемся спектре только одна из них, совпадающая с l _бл, будет иметь наиб. интенсивность (рис. 2), а интенсивность остальных линий l₁, l₂,..., l₆ меньше и определяется "огибающей" ф-цией J _д, что необходимо учитывать при обработке спектров.

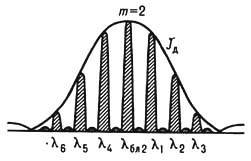
Рис. 2. Искажающее действие "огибающей" функции J _д на интенсивность результирующих интерференционных максимумов функции J_N в области l _бл2 спектра второго порядка.

Для оценки величины относит. искажений интенсивности регистрируемого спектра по сравнению с интенсивностью l _бл "огибающую" ф-цию (sinu/u)² можно преобразовать (из требования и =0и y + j = 2W) к виду

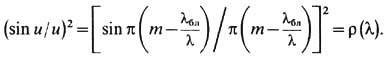
Для отражат. Э. это выражение обычно наз. относительным коэф. отражения Э. r(l) по отношению к величине r(l _бл1)=1, где l _бл1 - длина волны "блеска" в 1-м порядке спектра т =1. На рис. 3 приведены рассчитанные на ЭВМ графики ф-ции r(l) в зависимости от отношения l/l _бл для т=1,2, 3. Область полуширины ф-ции (sinu/u)² при и=+p/2, где r(l) = 0,405, наз. осн. областью концентрации излучения или областью энергетич. эффективности Э.: (Dl) _{эн m} = l _{бл m}4m/(4m²- 1) (рис. 3). В пределах этой области длин волн величина r(l) изменяется в интервале 0,405<r(l)< 1, т. е. почти в 2,5 раза. Величина (Dl) _{эн m} зависит от порядка спектра т: максимальна в 1 -м порядке (Dl) _{эн 1} =(⁴/₃)l _бл1 и быстро уменьшается в спектрах 2-го, 3-го и далее порядков. Поэтому Э. наиб. часто используется в условиях образования спектров 1-го порядка. Энергетич. область (Dl) _{эн 1} 1-го порядка спектра больше обычно используемой области дисперсии (Dl) _д, т. к. она свободна от переналожения спектров более высоких порядков т =2, 3, ... Расчёт показывает, что при т=1 величина r(l) в пределах области дисперсии изменяется в интервале 0,68 < r(l) < 1, т. е. в ~1,5 раза. Такие изменения r(l) возможны, если для данного исследуемого спектра Dl = l₂ - l₁ параметры Э. (W, d )и схема его установки выбраны так, чтобы выполнялось условие "блеска". Если условие "блеска" не выполняется, интервал изменения r(l) может быть больше, а величины r(l) неодинаковы на краях спектра. Поэтому выбор параметров Э. для проведения исследований в конкретной области спектра является важным. Если область спектра известна Dl = l₂ -l₁, то величина l _бл может быть определена из соотношения l _бл = 2l₁l₂/(l₁ + l₂); в частности, для октавы [для к-рой l₂ = 2l₁ и к-рая при т=1совпадает с областью дисперсии (Dl) _д] l_6л = (⁴/₃)l₁. При этом l _бл(l₁ + l₂)/2. Напр., для октавы видимой области (l₁ = 370 нм, l₂ = 740 нм) l _бл = 493,3 нм; для октавы ИК-области (l = 4-8 мкм) l _бл = 5,33 мкм.

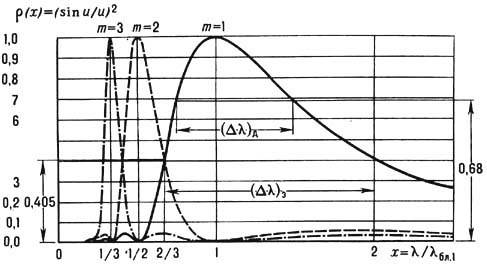
Рис. 3. График функции (sinu/u)² = r(x), x = l/l_6л1, в зависимости от отношения l/l_6л1; (Dl) _д - область дисперсии, (Dl) _э- область энергетической эффективности, (Dl) _д и (Dl) _э уменьшаются с увеличением т.

Постоянная Э. d и соответственно N₁ =1/d шт/мм выбираются из условия d>l₂ (l₂ -длинноволновая граница октавы в мкм). Для видимой области спектра обычно используются Э. с N₁ =1200 шт/мм (d=0,83 мкм = 1,12 l₂) и N₁.= 600 шт/мм (d=1,66 мкм = 2,25 l₂). Для ИК-области, где спектральный диапазон составляет неск. октав, используется Э. с N₁. от 300 до 4 шт/мм.

Зная d и l _бл, можно из ур-ний d(siny + sinj_m) = ml _бл и y + j_m = 2W при заданном значении угла падения y найти величину W. Напр., для октавы видимой области с Э. с N₁=600 шт/мм при y=10° и т=1имеем W = 8,6°. Для ИК-области 4-8 мкм N₁ = 100 шт/мм, т=1,y=10° имеем W=15,5°.

Если Э. имеет угол W, несколько отличающийся от расчётного при заданном угле падения y, то изменением угла y можно удовлетворить условию точного "блеска" при этом угле W.

При наиб. часто используемой автоколлимац. схеме установки Э. y = j = W и 2dsinyW = ml _бл величина W определяется однозначно: для октавы в видимой области спектра l _бл = 0,493 мкм, N₁ = 600 шт/мм, т=1,W = 8,5°.

Расчёт области концентрации излучения и рабочей области спектра, создаваемого Э., упрощается, если излучение характеризовать не длиной волны l, а волновым числом = 1/l см ^-1. При этом выражение для коэф. отражения Э. принимает вид

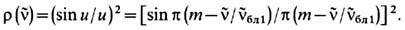
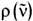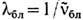В этом случае ф-ция оказывается симметричной относительно (рис. 4) и имеет одинаковый вид для всех порядков спектра, пересекающихся на уровне =0,405. Величина энергетич. эффективности , выраженная в единицах , не зависит от порядка спектра. При этом волновое число, соответствующее условию точного "блеска" равно ср. арифметическому крайних волновых чисел исследуемого спектра: ; соответственно . В пределах области дисперсии 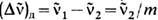коэф. отражения изменяется в пределах 0,68 < r() < 1 для всех порядков спектра (рис. 4).

Практически все серийно изготовляемые нарезные диф-ракц. решётки и реплики с них являются Э. с разл. числом N₁ и W для разл. областей оптич. спектра - от крайней УФ-области (l= 1 нм) до длинноволновой ИК-области (l=1000 мкм).

Для УФ-области используются Э. с N₁ = 3600, 2400, 1800 и 1200 шт/мм с углом W от 30' до 5° для области 1 -100 нм в схеме скользящего падения y = 80-85° и с углом W = 5- 20° для области 100-400 нм; для видимой области используются Э. с Ni = 1200-600 шт/мм с W = 8-20°; для разл. участков ИК-области - Э. с N₁ = 300, 200, 100, 50, 12, 6, 4 шт/мм с W = 5-20°.

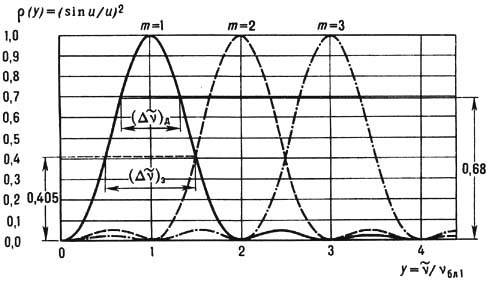
Рис. 4. График коэффициента отражения r(y) = (sinu/u)², ; - область дисперсии и -область энергетической эффективности, не зависящие от т.

Нарезные металлич. Э. и полимерные металлизир. реплики с них обладают поляризующим действием, т. к. коэф. отражения r(l) оказывается разным для составляющих электрич. вектора падающего излучения, направленных вдоль штрихов и перпендикулярно к ним. Поляризующее действие зависит от длины волны и соотношения d/l, что необходимо учитывать при исследовании спектров поляризованного излучения.

Лит.:Stamm R. F., Whale n J., Energy distribution of diffraction gratings as function of groove form, "JOSA", 1946, v. 36, p. 2; Герасимов Ф. М., Современные дифракционные решетки, "Оптико-механическая промышленность", 1965, № 11, с. 33; Тарасов К. И., Спектральные приборы, 2 изд., Л., 1977; Пей-сахсон И. В., Оптика спектральных приборов, 2 изд., Л., 1975; Малышев В. И., Введение в экспериментальную спектроскопию, М., 1979; Нагибина И. М., Интерференция и дифракция света, Л., 1985; Rowland H., Gratings in theory and practice, "Phil. Mag. J. Sci.", 1893, v. 35, p. 397. В. И. Малышев.