Akademik

- приближённый метод решения задач теории дифракции волн, пригодный для отыскания дифрагированного поля при прохождении волн через большие (в масштабах длины волны 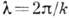) отверстия в экранах. Скалярное волновое поле 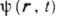(r - радиус-вектор, t - время), удовлетворяющее линейному волновому уравнению, можно выразить через значения 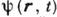и её первой производной на произвольной замкнутой поверхности 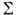, окружающей точку наблюдения (точку поля r_f ). Это одна из разновидностей Гюйгенса - Френеля принципа, согласно к-рому поле в точке r_f можно интерпретировать как результат суперпозиции вторичных волн, испускаемых условными источниками на 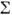.Строгое матем. выражение для поля было первоначально получено Г. Гельмгольцем (Н. Helm-holtz) и обобщено Г. Р. Кирхгофом в 1883.

В случае 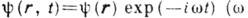- угл. частота) соответствующее интегральное представление имеет вид

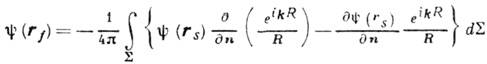
где 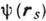- поле в точке r_s - на поверхности 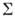, охватывающей точку r_f ; n - нормаль к 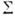, направленная в сторону точки наблюдения r_f;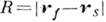. Т. о., роль вспомогат. источников на 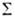играют величины 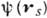и 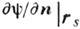. Для эл.-магн. волн им можно придать смысл электрич. или магн. зарядов и токов, распределённых по 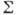. Строго говоря, для однозначного определения поля 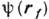достаточно задания на 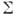либо 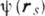, либо 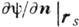, " так что их одноврем. задание должно быть согласованным с полным полем - падающим (внеш.) и дифрагированным. 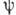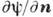Иногда допустимо задание и на 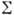, согласованное только с внеш. полем. В этом суть приближения в К. м. В частности, для задачи о падении волны на бесконечный идеально отражающий плоский экран с отверстием, размеры к-рого 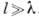, поверхность 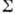составляется из трёх частей: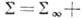 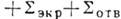. На участке 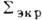. совмещённом с идеальным экраном, полагают 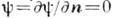, на участке 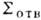, натянутом на раскрыв отверстия, 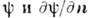соответствуют падающей невозмущённой волне, и, наконец, на участке 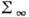, замыкающем поверхность по бесконечно удалённой полусфере, задают Зоммерфельда условия излучения. Это приближение исходит из картины искажения экраном падающего поля, соотв. геом. оптике, и потому оно тем точнее, чем больше размеры отверстия. Такой рецепт задания поля наз. граничными условиями Кирхгофа и составляет основу К. м. в теории дифракции. При этом ф-ция 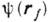, определяемая интегральным представлением, хорошо соответствует точному решению вблизи освещённой области, но может давать заметные отклонения вдали от неё. К. м. приводит к строгому решению задачи для источников, заданных по падающему полю на 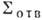и дополненных эквивалентными линейными зарядами и токами для компенсации разрывов в распределени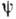и и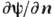

К. м. применяется для приближённого отыскания скалярных полей разл. природы; существуют обобщения на случай векторных и тензорных волновых полей.

Лит.: Хенл X., Mayа А., Вестпфаль К., Теория дифракции, пер. с нем., М., 1964; Борн М., Вольф Э., Основы оптики, пер. с англ., 2 изд., М., 1973; Виноградова М. Б., Руденко О. В., Сухоруков А. П., Теория волн, М., 1979; Ваганов Р. Б., Каценеленбаум Б. 3., Основы теории дифракции, М., 1982. Ю. А. Данилов.