Akademik

- количеств. характеристика, описывающая отклонение кривой, поверхности, риманова пространства и др. соответственно от прямой, плоскости, евклидова пространства и др. Обычно понятие К. вводится локально, т. е. в каждой точке. В декартовых координатах 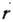= ( х, у )плоская кривая задаётся параметрически: 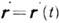, 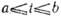(для кривой, заданной ф-цией y=f(x), параметром служит координата х). Среди всех возможных параметров наиб. удобен натуральный, равный длине кривой:

Для натурального параметра скорость 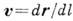- единичный вектор, меняющий лишь направление, а величина ускорения 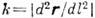наз. К. Для произвольного параметра 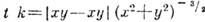. Радиусом кривизны наз. число k^-1. В случае пространственной кривой кроме К. требуется ещё одна характеристика - кручение. Для такой кривой единичный вектор n= = наз. нормалью, а векторное произведение 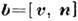- бинормалью. Вместе с они образуют ортогональный репер, вращение к-рого при движении вдоль кривой описывается ф-лами Френе:

коэф. и наз. кручением. Кривизна поверхности определяется след. образом. Через нормаль к поверхности в данной точке проводят всевозможные плоскости. Сечения поверхности этими плоскостями наз. нормальными сечениями, а К. нормальных сечений в этой точке - нормальными К. Макс. и мин. из нормальных К. наз. главными К. Если k₁ и k₂ - главные К., то величины K = k₁k₂. и М=(k₁+k₂)/2 наз. соответственно полной (или гауссовой) кривизной и средней кривизной поверхности в данной точке. Напр., со ср. кривизной поверхности жидкости связано избыточное давление газа (см. Лапласа закон), Кривизну риманова пространства обычно характеризуют с помощью кривизны тензора, или Риманатензора.

Лит.: Рашевский П. К.. Риманова геометрия и тензорный анализ, 3 изд., М., 1967; Фок В. А., Теория пространства, времени и тяготения, 2 изд., М., 1961; Дубровин Б. А., Новиков С. П., Фоменко А. Т., Современная геометрия, 2 изд.. М.. 1986. В. И. Алхимов.