- МАТРИЦА
-
- прямоугольная таблица

состоящая из т строк и n столбцов; её паз. M. размера
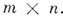 Элементами(первый индекс указывает номер строки, второй
Элементами(первый индекс указывает номер строки, второй 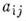 - номер столбца) M. могут быть числа, ф-ции пли др. величины, над к-рыми можно производить алгебраич. операции. M. также обозначают как
- номер столбца) M. могут быть числа, ф-ции пли др. величины, над к-рыми можно производить алгебраич. операции. M. также обозначают как 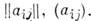 Наряду с конечными M. рассматривают M. с бесконечным числом строк или столбцов.
Наряду с конечными M. рассматривают M. с бесконечным числом строк или столбцов.M. размера
 наз. столбцом, а размера-
наз. столбцом, а размера- строкой. M., все элементы к-рой равны нулю, наз. нулевой M. и обозначается О. M. размера
строкой. M., все элементы к-рой равны нулю, наз. нулевой M. и обозначается О. M. размера  наз. квадратной M. порядка п. У квадратной M. число строк равно числу столбцов. Квадратная M.
наз. квадратной M. порядка п. У квадратной M. число строк равно числу столбцов. Квадратная M.  наз. треугольной, если а ij =0 при
наз. треугольной, если а ij =0 при  , "строго треугольной, если
, "строго треугольной, если  при
при 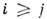 , диагональной, если
, диагональной, если  при
при 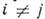 . Диагональная M. обычно обозначается diag
. Диагональная M. обычно обозначается diag  . Если все
. Если все 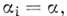 получают скалярную M. При
получают скалярную M. При 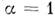 M. наз. единичной и обозначается I или E. В квадратной M. диагональ, проведённая из верхнего левого угла в нижний правый угол, наз. гл. диагональю.
M. наз. единичной и обозначается I или E. В квадратной M. диагональ, проведённая из верхнего левого угла в нижний правый угол, наз. гл. диагональю.Квадратная M. наз. неособенной (невырожденной), если она имеет единств, обратную M.
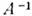 , определяемую условиями
, определяемую условиями 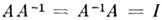 . В противном случае А- особенная (вырожденная) M. Квадратная M. является неособенной в том и только в том случае, когда её определитель,del А, отличен от нуля. Понятие M. впервые появилось в сер. 19 в. в работах У. P. Гамильтона (W. R. Hamilton) и А. Кэли (A. Cayley).
. В противном случае А- особенная (вырожденная) M. Квадратная M. является неособенной в том и только в том случае, когда её определитель,del А, отличен от нуля. Понятие M. впервые появилось в сер. 19 в. в работах У. P. Гамильтона (W. R. Hamilton) и А. Кэли (A. Cayley).Действия над матрицами. Суммой или разностью двух
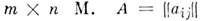 и
и  наз.
наз.  M.
M.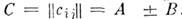 , где
, где  Произведением M ".
Произведением M ". 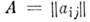 на число a наз. M. с элементами ффaaij.
на число a наз. M. с элементами ффaaij.Перемножать две M. можно только тогда, когда число столбцов в 1-м сомножителе яавно числу строк во 2-м. Если
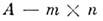 M., a
M., a M., то
M., то  M.
M.С с элементами
 наз. произведением M.
наз. произведением M.Ap Вp обозначается:
 . Если существуют оба произведения AB и BA (это, в частности, будет всегда, если А и В- квадратные M. одного и того же порядка), то, вообще говоря,
. Если существуют оба произведения AB и BA (это, в частности, будет всегда, если А и В- квадратные M. одного и того же порядка), то, вообще говоря,  В результате перемножения двух M. можно получить нулевую M., хотя ни одна из перемножаемых M. не является нулевой. Невырожденные M. порядка
В результате перемножения двух M. можно получить нулевую M., хотя ни одна из перемножаемых M. не является нулевой. Невырожденные M. порядка 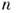 образуют группу относительно умножения, она наз. полной линейной группой
образуют группу относительно умножения, она наз. полной линейной группой 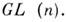
Определённые выше операции обладают след, свойствами:
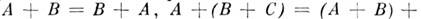
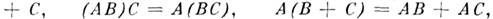

Транспонированием M.
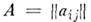 размера
размера  наз. замена её строк столбцами (1-я строка заменяется на 1-й столбец, 2-я строка на 2-й столбец и т. д.), т. е. это переход к M.
наз. замена её строк столбцами (1-я строка заменяется на 1-й столбец, 2-я строка на 2-й столбец и т. д.), т. е. это переход к M. 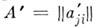 размера
размера  такой, что
такой, что 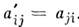 Комплексным сопряжением M.
Комплексным сопряжением M. наз. переход к M.
наз. переход к M.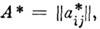 где
где  означает комплексное сопряжение.
означает комплексное сопряжение.Эрмитовым сопряжением M.
 размера
размера  наз. переход к M.
наз. переход к M.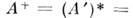
 размера
размера 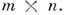 M.
M. наз. эрмитово сопряжённой с M. А. Имеют место след, соотношения:
наз. эрмитово сопряжённой с M. А. Имеют место след, соотношения: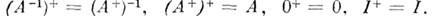
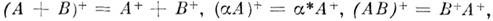
Квадратные матрицы. Квадратная M. А наз.: симметричной, если
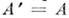 ; антисимметричной, если
; антисимметричной, если 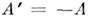 ; эрмитовой (самосопряжённой), если
; эрмитовой (самосопряжённой), если 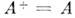 ; антиэрмитовой, если
; антиэрмитовой, если  ; ортогональной, если
; ортогональной, если 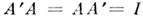 ; унитарной, если
; унитарной, если  I; унимодулярной, если
I; унимодулярной, если  . Для каждой M. А с комплексными элементами
. Для каждой M. А с комплексными элементами 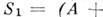
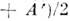 есть симметричная,
есть симметричная, антисимметричная,
антисимметричная,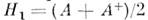 - эрмитова и H2
- эрмитова и H2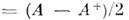 - антиэрмитова M.
- антиэрмитова M.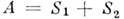 - разложение (единств.) данной M. в сумму симметричной и антисимметричной M.
- разложение (единств.) данной M. в сумму симметричной и антисимметричной M.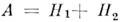 - разложение
- разложение (единств.) данной M. в сумму эрмитовой и антиэрмитовой M.
Существует т. н. полярное разложение
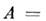
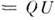 M. А в произведение эрмитовой M.
M. А в произведение эрмитовой M.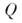 и унитарной
и унитарной  однозначно определяется условием
однозначно определяется условием 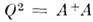 , a M. U однозначно определяется в том и только в том случае, если А - невырожденная M. (это разложение аналогично представлению комплексного числа в ппде
, a M. U однозначно определяется в том и только в том случае, если А - невырожденная M. (это разложение аналогично представлению комплексного числа в ппде 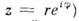
M. А, для к-рой выполняется условие
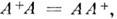 наз. нормальной M. M. А нормальна тогда и только тогда, когда её можно преобразовать в диагональную M. D унитарным преобразованием, т. е.
наз. нормальной M. M. А нормальна тогда и только тогда, когда её можно преобразовать в диагональную M. D унитарным преобразованием, т. е.
M. А наз. подобной M.
 если существует такая неособенная M. T (преобразующая M.), что
если существует такая неособенная M. T (преобразующая M.), что 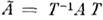 ; А,
; А,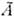 я T должны быть M. одного и того же порядка. Переход от M. А к M.
я T должны быть M. одного и того же порядка. Переход от M. А к M. наз. преобразованием подобия. При каждом преобразовании подобия сохраняются инварианты матрицы. Две подобные M. имеют один и тот же ранг, один и тот же след, один и тот же определитель. Все подобные M. образуют класс подобных матриц, и важной задачей теории M. является выбор M. простейшего вида в этом классе - приведение M. к канонич. форме. Решение этой задачи тесно связано с нахождением собств. значений M. (см. ниже).
наз. преобразованием подобия. При каждом преобразовании подобия сохраняются инварианты матрицы. Две подобные M. имеют один и тот же ранг, один и тот же след, один и тот же определитель. Все подобные M. образуют класс подобных матриц, и важной задачей теории M. является выбор M. простейшего вида в этом классе - приведение M. к канонич. форме. Решение этой задачи тесно связано с нахождением собств. значений M. (см. ниже).Любая M. подобна треугольной M., диагональные элементы к-рой - собств. значения M. Матрицу А можно преобразованием подобия с унитарной преобразующей матрицей T привести к диагональному виду в том и только в том случае, если А подобна нек-рой нормальной M. В этом случае диагональные элементы M.
 являются собств. значениями M. Эрмитовы и унитарные M. (а потому действительные и симметричные пли ортогональные M.) представляют собой частные случаи нормальных M., поэтому все они приводятся к диагональному виду.
являются собств. значениями M. Эрмитовы и унитарные M. (а потому действительные и симметричные пли ортогональные M.) представляют собой частные случаи нормальных M., поэтому все они приводятся к диагональному виду.Теория M. тесно связана с теорией линейных преобразований векторных пространств (см. Линейный оператор).
Собственными значениями (собств. числами, характеристич. числами) M.
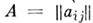 наз. корни характеристического уравнения матрицы
наз. корни характеристического уравнения матрицы  . M. удовлетворяет своему характеристич. ур-нию. Если
. M. удовлетворяет своему характеристич. ур-нию. Если 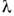 - собств. значение M. А порядка п, то существует ненулевой столбец (вектор-столбец) k такой, что
- собств. значение M. А порядка п, то существует ненулевой столбец (вектор-столбец) k такой, что  . Этот вектор-столбец наз. собственным (характеристическим) вектором M. А, соответствующим собств. значению
. Этот вектор-столбец наз. собственным (характеристическим) вектором M. А, соответствующим собств. значению 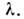 Спектром (собств. значений) M. А наз. множество всех её собств. значений. Собств. значения M. А обладают след, свойствами:
Спектром (собств. значений) M. А наз. множество всех её собств. значений. Собств. значения M. А обладают след, свойствами:
где Т rA = след M. А. Следовательно, если хотя бы одно собств. значение равно нулю, то M. является особенной (вырожденной).
Если M. А порядка n имеет n разл. собств. значений
 , то существует n независимых собств. векторов
, то существует n независимых собств. векторов 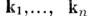 , соответствующих этим собств. значениям. Если А- действительная и симметричная M. и если
, соответствующих этим собств. значениям. Если А- действительная и симметричная M. и если  - вектор-строка, получающаяся транспонированием вектора-столбца
- вектор-строка, получающаяся транспонированием вектора-столбца  . Если M. А - невырожденная, то собств. значениями M.
. Если M. А - невырожденная, то собств. значениями M. являются
являются 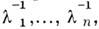 а собств. векторами по-прежнему векторы
а собств. векторами по-прежнему векторы  Если-
Если- наиб. модуль h собств.
наиб. модуль h собств.значений M. А порядка n, то при
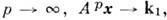 где c- произвольный вектор-столбец. Для действительной ортогональной M. А
где c- произвольный вектор-столбец. Для действительной ортогональной M. А для всех I. Если А- симметричная M. и не все собств. значения различны, всё равно можно найти h взаимно ортогональных собств. векторов. Если каждый такой вектор kj нормирован, т. е. умножен на
для всех I. Если А- симметричная M. и не все собств. значения различны, всё равно можно найти h взаимно ортогональных собств. векторов. Если каждый такой вектор kj нормирован, т. е. умножен на 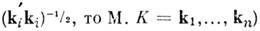 ортогональна и
ортогональна и 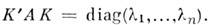 Вообще,
Вообще,если M. А порядка h имеет h разл. собств. значений
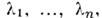 к-рым соответствуют независимые собств. векторы
к-рым соответствуют независимые собств. векторы 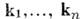 , то преобразует
, то преобразует
А в диагональную M.:
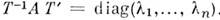 . Если не все h собств. значений различны, то такое преобразование может оказаться невозможным.
. Если не все h собств. значений различны, то такое преобразование может оказаться невозможным.Если H- эрмитова M. порядка п, то её собств. значения всегда действительны и всегда можно найти п собств. векторов
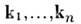 таких, что
таких, что 
Унитарная M.
 преобразует Н к диагональному виду.
преобразует Н к диагональному виду.С каждой M. А порядка n связана квадратичная форма от n комплексных переменных
 образующих столбец х:
образующих столбец х: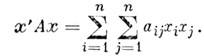
Эрмитова форма
 где H - эрмитова M., принимает только действит. значения; она наз. положительно определенной или неотрицательной, если
где H - эрмитова M., принимает только действит. значения; она наз. положительно определенной или неотрицательной, если  или
или  для каждого набора
для каждого набора 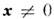 .
. Аналитич. функцию матрицы A порядка n определяют при помощи ряда
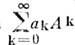 по степеням А.
по степеням А.Каждый такой ряд можно свести к многочлену га-й степени от А, т. к. M. А удовлетворяет своему характе-ристич. ур-нию. M. А наз. нильпотентной, если
 при нек-ром целом положительном k.
при нек-ром целом положительном k.M. А тогда и только тогда нильпотентна, когда все её собств. значения равны нулю.
M., имеющую более чем одну строку и столбец, можно разбить на меньшие прямоугольные подматрицы (блоки), проведя между столбцами и (или) строками прямые линии. Две соответствующим образом разбитые M. А и В размера
 можно перемножить, пользуясь входящими в них подматрицами как элементами в обычной ф-лс произведения M.; получающиеся таким путём элементы произведения являются подматрицами M. AB размера
можно перемножить, пользуясь входящими в них подматрицами как элементами в обычной ф-лс произведения M.; получающиеся таким путём элементы произведения являются подматрицами M. AB размера  M., разбитую на блоки, наз. клеточной (блочной) M. Прямым (внешним, кронекеровским) произведением М. А к В наз. блочная M. С= A х В, блоки к-рой имеют вид В, С и D существуют произведения AC и BD, то
M., разбитую на блоки, наз. клеточной (блочной) M. Прямым (внешним, кронекеровским) произведением М. А к В наз. блочная M. С= A х В, блоки к-рой имеют вид В, С и D существуют произведения AC и BD, то 
 . Если M. А имеет вид
. Если M. А имеет вид 
т. е. является диагональной M. с диагональными элементами в виде квадратных подматриц
 то такая M. наз. клеточно-диагональной. В этом случае
то такая M. наз. клеточно-диагональной. В этом случае 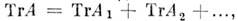

 ... Клеточно-диагональной M. является нормальная (жорданова) форма, к к-рой можно преобразованием подобия привести любую M. При этом в каждой диагональной клетке вдоль гл. диагонали повторяется одно и то же число, а параллельный ряд над гл. диагональю состоит из 1. Все остальные элементы в диагональных клетках равны нулю:
... Клеточно-диагональной M. является нормальная (жорданова) форма, к к-рой можно преобразованием подобия привести любую M. При этом в каждой диагональной клетке вдоль гл. диагонали повторяется одно и то же число, а параллельный ряд над гл. диагональю состоит из 1. Все остальные элементы в диагональных клетках равны нулю:
Важную роль играют M. в квантовой механике, где динамнч. наблюдаемым величинам сопоставляют эрмитовы M., собств. значения к-рых соответствуют экспериментально наблюдаемым значениям этих фпз. величин. При описании квантовомеханич. явлений, в к-рых участвуют частицы, обладающие спином, используют Паули матрицы и Дирака, матрицы. В квантовой теории поля, где существенны разл. группы симметрии, рассматривают матричные представления групп.
MH. задачи по обращению M., нахождению их собств. значений и т. д., возникающие в физ. исследованиях, решают с помощью ЭВМ.
Лит.: Мальцев А. И., Основы линейной алгебры, 4 изд., M., 1975; Гантмахер F. Р., Теория матриц, 4 изд., M., 1988; Мишина А. П., Проскуряков И. В., Высшая алгебра, 2 изд., M., 1965; Боревич 3. П., Определители и матрицы, 3 изд., M., 1988; Беллман Р., Введение в теорию матриц, пер. с англ., 2 изд., M., 1976; Маркус M., Mини X., Обзор по теории матриц и матричных неравенств, пер. с англ., M., 1972. С. И. Азаков.
Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.
.