Akademik

- обобщение понятия расстояния между точками евклидова пространства на множества, в к-рых можно ввести M. (метрич. пространства). Для точек х, у такого пространства M.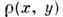- это вещественная неотрицат. ф-ция, удовлетворяющая условиям:

1)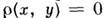лишь при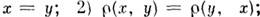

3)

Вид M. зависит как от самого пространства, так и от выбора системы координат в нём. Простейший пример M. - расстояние 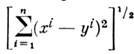в декартовых координатах евклидова пространства. M. евклидова пространства в криволинейных координатах и М. риманова пространства определяются метрическим тензором.M. гильбертова пространства задаётся его нормой (или скалярным произведением). Понятие M. применяется и в тех случаях, когда не все условия 1-3 выполнены: напр., если 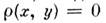не только при х = у, то r наз. псевдометрикой. Если M. не является положительно определённой, то её наз. индефинитной метрикой', физ. примером такой ситуации служит M. пространства Минковского в относительности теории. В. П. Павлов.