- ПЛОТНОСТЬ СОСТОЯНИЙ
-
- число возможных физически неэквивалентных энергетич. состояний в малом интервале энергии
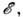 отнесённое к ширине интервала
отнесённое к ширине интервала 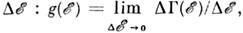 где
где 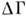 - число состояний с энергиями между
- число состояний с энергиями между 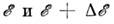 (с учётом возможного вырождения энергетич. состояний). Для колебат. степеней свободы системы часто имеют в виду спектральную П. с.
(с учётом возможного вырождения энергетич. состояний). Для колебат. степеней свободы системы часто имеют в виду спектральную П. с.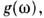 определяемую по числу состояний на интервал частот
определяемую по числу состояний на интервал частот 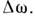 В этом случае
В этом случае 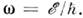
П. с. имеет смысл вводить, либо если системаобладает непрерывным энергетич. спектром, либо если спектр дискретен, когдарасстояние между соседними энергетич. уровнями мало по сравнению с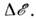 Если состояния системы определяются широко разнесёнными по
Если состояния системы определяются широко разнесёнными по 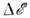 дискретными уровнями, каждый из к-рых расщепляется в области, узкие посравнению с расстоянием между уровнями, то вводят П. с. вблизи каждогодискретного уровня. Это имеет место, напр., при движении электронов в сильномквантующем магн. поле (см. Ландау уровни, Лифшица- Онсагераквантование). Для свободных нерелятивистских частиц со спином . состояния характеризуются импульсом р и проекцией спина, а энергия
дискретными уровнями, каждый из к-рых расщепляется в области, узкие посравнению с расстоянием между уровнями, то вводят П. с. вблизи каждогодискретного уровня. Это имеет место, напр., при движении электронов в сильномквантующем магн. поле (см. Ландау уровни, Лифшица- Онсагераквантование). Для свободных нерелятивистских частиц со спином . состояния характеризуются импульсом р и проекцией спина, а энергия 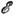 = р 2/2т (т - масса) П. с. зависит только от р:
= р 2/2т (т - масса) П. с. зависит только от р: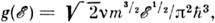 гдемножитель v = 2s + 1 учитывает вырождение по спину s. Для квазичастиц твёрдого тела эта зависимость является более сложной, напрю для электронов проводимости с энергетич. спектром
гдемножитель v = 2s + 1 учитывает вырождение по спину s. Для квазичастиц твёрдого тела эта зависимость является более сложной, напрю для электронов проводимости с энергетич. спектром 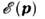
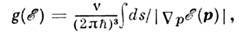
где интегрирование ведётся по изоэнергетич. поверхности
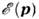 = const в пространстве квазиимпульсов, ds- элемент площади на этойповерхности;
= const в пространстве квазиимпульсов, ds- элемент площади на этойповерхности;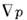 - градиент в пространстве квазиимпульсов. Для спектральной П. с.
- градиент в пространстве квазиимпульсов. Для спектральной П. с.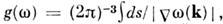 где k - волновой вектор, а интегрирование ведётся по поверхности
где k - волновой вектор, а интегрирование ведётся по поверхности 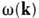 = const. Подынтегральные выражения для П. с. имеют особенности в точках, в к-рых групповые скорости
= const. Подынтегральные выражения для П. с. имеют особенности в точках, в к-рых групповые скорости 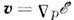 обращаются в 0. Эти точки наз. критическими, а соответствующие особенностив
обращаются в 0. Эти точки наз. критическими, а соответствующие особенностив 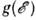 - ВанХова особенностями.
- ВанХова особенностями.
Информация о П. с. существенна при определениитермодинамич. характеристик твёрдых тел (теплоёмкость, магн. восприимчивостьи др.), задаваемых интегралами по энергии от соответствующих микроскопич. величин, умноженных на ф-цию распределения и П. с. На кинетич. характеристики(электропроводность, теплопроводность и др.) также влияет П. с. При этомдля вырожденных систем, ферми-частиц, напр. электронов в металлах, особенноважна П. с. на поверхности Ферми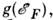 входящая непосредственно в виде множителя в большинство макроскопич. характеристиксистемы. Для полупроводников наиб. важна П. с. вблизи дна зоны проводимостии потолка валентной зоны.
входящая непосредственно в виде множителя в большинство макроскопич. характеристиксистемы. Для полупроводников наиб. важна П. с. вблизи дна зоны проводимостии потолка валентной зоны.
Для систем, к-рые подчиняются случайномураспределению в пространстве, в частности для конденсиров. неупорядоченныхсистем (жидкости, стёкла, аморфные вещества и пр.), П. с. являетсяосн. характеристикой энергетич. спектра. Т. к. П. с. является самоусредняющейсявеличиной (см. Мезоскопика неупорядоченной системы), то можно оперироватьс П. с., усреднённой по пространств. распределениям частиц (в то времякак понятие усреднённого энергетич. спектра лишено смысла).Лит. см. при ст. Зонная теория.
А. Э. Мейерович.
Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.
.