Akademik

- электронная проводимость разреженной замагниченной плазмы поперёк маги, поля, обусловленная столкновениями электронов не с тяжёлыми частицами (атомами, ионами) в объёме, а столкновениями с поверхностями (стенками), пересекающими магн. силовые линии. Проводимость поперёк магн. поля возникает при наличии возмущения дрейфовой скорости частиц. П. п. может быть связана как с "диффузным", так и с "квазизеркальным" рассеянием электронов.

Пристеночная проводимость с диффузным рассеянием. Если поверхность гладкая (т. е. размер неровности 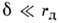- дебаевского радиуса экранирования )и скорость электрич. дрейфа параллельна ей, то 11. п. создают те электроны, к-рые "пронизывают" дебаевский слой и диффузно рассеиваются непосредственно на поверхности. Это имеет место, напр., в осесимметричных системах с внешними (полоидальными) магн. и электрич. полями.

Рис. 1. Схема взаимодействия электронов с поверхностью: а- токовые слои в идеализированной модели рассеяния моноэнергетических электронов стенкой (кривая со стрелками - проекции траектории движения электрона, отражённого стенкой, на плоскость ху); б- распределение пристеночного тока при наличии разброса скоростей электронов.

Возникновение "диффузной" П. п. можно рассмотреть на простой модели (рис. 1, а): плоская поверхность ( у= 0), дебаевский слой пренебрежимо тонок, магн. поле H однородно и перпендикулярно поверхности, а электрич. поле E в объёме плазмы параллельно
поверхности и направлено вдоль оси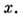 Электроны при падении на стенку полностью теряют скорость. Возвращаясь в объём, они разгоняются в дебаевском слое (скачок потенциала 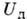) и приобретают скорость 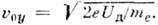Двигаясь далее с такой скоростью в объемных электрич. и магн. полях, электроны начинают выписывать циклоиду вдоль осе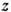й и 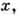смещаясь со скоростью 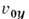вдоль магн. поля. Проекция этого движения на плоскость ух имеет вид, приведённый на рис. 1: объём канала разбивается на систему плоскопараллельных n слоев с чередующимся противоположным направлением движения электронов. При этом толщина каждого слоя 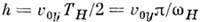(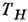- период ларморовского вращения). Если в канале укладывается целое число слоев, то переносимый ток будет равен либо нулю (число слоев чётное), либо будет максимальным (при нечётном числе слоев). Отнесённый к 1 см длины вдоль оси он равен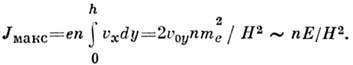

Поскольку в реальных условиях отражённые электроны не имеют одинаковых скоростей, плоскопараллельные слои имеют разную толщину и вследствие этого разно-скоростные электроны, находящиеся на одном расстоянии от стенки, будут иметь разное направление движения. В результате в плазменном канале оказываются чётко выраженными 2-3 осцилляции (около стенок), а остальные затухают при удалении от них (рис. 1, б).

Пристеночная проводимость с "квазизеркальным" рассеянием реализуется на шероховатой поверхности или на гладкой поверхности, если скорость дрейфа ей не параллельна. Зеркальное отражение электрона от дебаевского скачка потенциала приводит к изменению дрейфовой скорости. В этом случае (в отличие от диффузного) в П. п. втягиваются все электроны, достигающие дебаевского слоя вне зависимости от того, рассеются они на самой поверхности или нет.

Перенос электронов путём рассеяния на стенках является своеобразным обобщением кнудсеновского течения газа в трубах (см. Динамика разреженных газов). Различие состоит в том, что электрон находится в эл.-магн. полях и поэтому между столкновениями двигается не по прямой, а по сложной траектории. Кроме того, при кнудсеновском течении каждая частица сталкивается со стенкой, тогда как в плазменном объёме может существовать группа электронов, к-рая вообще не достигает стенок, т. к. заперта в объёме полями. Ур-ние для ф-ции распределения электронов, рассеиваемых стенкой при отсутствии столкновений в объёме, имеет вид:

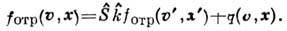
Здесь 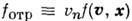- распределение по скоростям потока частиц, идущих от стенки, 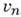- нормальная составляющая скорости, 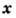- координата точки на поверхности объёма, 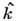- оператор "переноса" частиц от одной точки 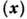к другой 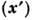(в известных E, H полях
он определяется из решения ур-ния Власова),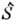 - оператор рассеяния частиц на поверхности, q- плотность эмиссии (поглощения) электронов.

Проводимость, очень напоминающая пристеночную, может наблюдаться и на ионах, если повторная ионизация нейтрального атома, возникшего при попадании иона на стенки, происходит на расстояниях меньше ларморовского радиуса.

Рис. 2. Распределение плотности продольного электронного тока 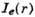по радиусу в канале ускорителя с замкнутым дрейфом электронов на расстоянии 13 мм от анода (внутренний радиус канала r = 20 мм, внешний -36 мм).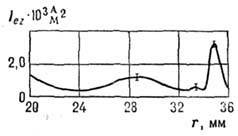

Аналогом П. п. является т. н. статический скин-эффект, к-рый наблюдается в охлаждённых до гелиевых темп-р металлах, находящихся во внеш. магн. поле.

Явление П. п. было предсказано А. И. Морозовым и обнаружено экспериментально на плазменном ускорителе с замкнутым дрейфом электронов. Он представляет собой цилиндрич. канал, перпендикулярно стенкам к-рого создаётся квазирадпальное магн. поле, а вдоль системы между анодом и катодом приложено продольное электрич. поле. Ускоритель работал на Хе и имел характерные параметры: 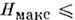200 Э, 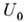= 200 В,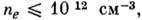 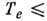20 эВ, 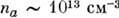^; при расстоянии между стенками 16 мм и длине канала 40 мм. Радиальное распределение продольного электронного тока, полученное с помощью зонда, имело осциллирующую структуру (рис. 2).

Лит.: Морозов А. И., Эффект пристеночной проводимости в хорошо замагниченной плазме, "Ж. прикл. мех. и техн. физ.", 1968, в. 3, с. 19; Морозов А. И., Шубин А. П., Кинетика электронов в режиме пристеночной проводимости, "Физ. плазмы", 1984, т. 10, в. 6, с. 1262; Бугрова А. И., Морозов А. И., Харчевников В. К., Исследование структуры пристеночного слоя с помощью зондов различных размеров, "ЖТФ", 1985, т. 55, в. 6, с. 1072. А. И. Бугрова.