Akademik

- функционал 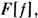функциональные производные к-рого по аргументу 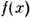дают изучаемый набор ф-ций

Формально П. ф. представляется рядом

а ф-ции наз. коэффициентными ф-циями разложения Функцией, аргумент может быть набором многокомпонентных ф-ций многих переменных: = =,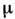= 1,..., т. Целесообразность введения П. ф. для набора ф-ций 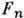в том, что многие их свойства переносятся на 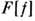и компактно записываются на языке П. ф. Роль П. ф. в квантовой теории поля основана на той, что в наиб. употребительном в ней Фока представлении векторам состояния Ф и операторам 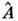по самому их построению отвечают П. ф. (для простоты берётся случай скалярного поля)

где 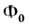-фоковский вакуум, 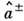-операторы рождения и уничтожения частиц с 3-импульсом k. П. ф. наз. нормальным символом оператора , а его разложение получается заменой на комплексно сопряжённые ф-ции а*, а из нек-рого гильбертова пространства. При этом Ф[ а*] - П. ф. для волновых ф-ций 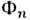n -ча-стичных состояний, а А[а*, а]- П. ф. для матричных элементов 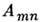оператора в фоковском базисе.

В релятивистской теории в качестве функцион. аргумента берётся нормальный символ 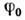оператора свободного поля: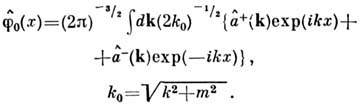

Нормальный символ матрицы рассеяния

является П. ф. её коэффициентных ф-ций 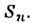Поскольку как и удовлетворяют ур-нию свободного поля,и определены лишь на поверхности энергии. Для формулировки причинности вводят расширенный нормальный символ 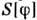, аргумент к-рого уже не удовлетворяет ур-нию свободного поля. В возмущений теории этот П. ф. выражается ф-лой Хори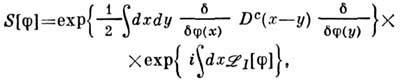

где 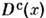- причинная ф-ция Грина ( пропагатор),

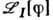- нормальный символ лагранжиана взаимодействия. Эта ф-ла компактно записывает результат применения Вика теоремы к стандартному выражению для S -матрицы в теории возмущений:

Заменой функцион. аргумента у 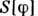можно получить П. ф. для Грина функций

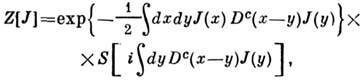
где J(x)- внеш. источник поля. Функционал W[J] = = lnZ[J]является П. ф. для связных ф-ций Грина. Лежандра преобразование W[J]даёт П. ф. для сильно связных ф-ций Грина, называемый иногда эфф. действием. На языке П. ф. легко выводятся и компактно формулируются У орда тождества и нек-рые др. соотношения между ф-циями Грина.

П. ф. используется и в статистической физике. Напр., введём s-частичные ф-ции распределения N- ча - стичной системы:

где V- объём,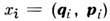, а полная ф-ция распределения w_N удовлетворяет Лиувилля уравнению-

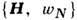=. с Гамильтона функцией H =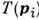I +. Тогда всю цепочку Боголюбова уравне ний для порождает (в термодинамич. пределе V, N, V/N =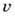=const) ур-ние

для П. ф.

а сами 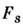выражаются через него ф-лами

Лит.: Березин F. А., Метод вторичного квантования, 2 изд., М., 1986; Васильев А. Н., Функциональные методы в квантовой теории поля и статистике, Л., 1976; Славнов А. А.,Фаддеев Л. Д., Введение в квантовую теорию калибровочных полей, 2 изд., М., 1988; Ициксон К., 3 ю-. бер Ж.-Б., Квантовая теория поля, пер. с англ., т. 1-2, М., 1984. А. М. Малокостов, В. П, Павлов,