Akademik

(взаимодействие Рудермана - Киттеля- Касуя - Иосиды) - косвенное обменное взаимодействие между магн. ионами, осуществляемое через коллективизиров. электроны проводимости. РККИ-о. в. возникает в металлах и полупроводниках, где коллективизиров. электроныпроводимости выступают посредниками обменного взаимодействия (ОВ) ионов, обладающих локализов. спинами, незаполненных d- и f- оболочек. В частности, РККИ-о. в. наблюдаются в редкоземельных металлах и их сплавах. Благодаря сильной локализации электронов 4f -оболочек перекрытиеволновых ф-ций электронов соседних ионов слишком мало и прямое ОВ в такихвеществах не может обеспечивать наблюдаемое магн. упорядочение.

Идея косвенного ОВ посредством коллективизиров. носителей магн. моментавысказана М. Рудерманом и Ч. Киттелем [1] в работе, посвящённой теории сверхтонкоговзаимодействия. Т. Касуя [2] и К. Иосида [3] предположили, что механизмвозникновения эффективного ОВ между магн. моментами ионов аналогичен механизмувозникновения эфф. взаимодействия между ядерными спинами.

Локализов. спин, погружённый в «облако» электронов проводимости, создаётспиновую поляризацию этого облака, причём поляризация носит осциллирующий(в пространстве) характер. Спины электронов проводимости стремятся экранироватьлокализов. спин, подобно тому как заряд электронов стремится экранироватьположит, заряд погружённого в их облако иона. Аналогично тому, как приэкранировании положит. заряда в облаке электронов возникают довольно слабозатухающие с расстоянием осцилляции концентрации электронов, возникаюти слабо затухающие осцилляции спиновой поляризации. Эти осцилляции воспринимаютсядругими локализов. спинами в той области пространства, где они локализованы, и в результате появляется осциллирующий потенциал взаимодействия междуспинами.

Интеграл эффективного РККИ-о. в. можно рассчитать в рамках микроскопической s- f -обменной модели. Локализованные на ионах электроны частичнозаполненных оболочек описываются локализованными (атомными) волновыми ф-циями(f -подсистема), электроны проводимости описываются блоховскими функциями(s-подсистема) и наз. блоховскими электронами. Прямым f -f -ОВможно пренебречь, т. к. расстояние между соседними ионами превышает радиус f -оболочки. Гамильтониан системы можно записать в виде

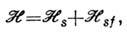
где 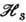- гамильтониан подсистемы электронов проводимости, а 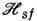- гамильтониан s - f-OB: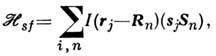

здесь 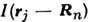- интеграл ОВ s-электрона со спином s_j, находящегосяв точке с радиусом-вектором rj, с f -электронами n -гоиона, обладающего результирующим спином S_n и локализованногов точке с радиусом-вектором R_n. Оценки величины I показывают, что I ~ 10^-14-10^-13 эрг, в то время как ферми-энергия дляэлектронов проводимости 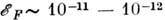эрг, т. о., параметр 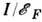можно считать малым. Применив возмущений теорию по этому маломупараметру, можно рассчитать эфф. интеграл ОВ. Поправка к энергии в первомпорядке по теории возмущений не возникает, если предположить, что в основномсостоянии электроны проводимости находятся в неполяризов. состоянии, т. к. имеется равное число электронов со спинами, направленными вдоль и противнамагниченности. Поправка второго порядка имеет вид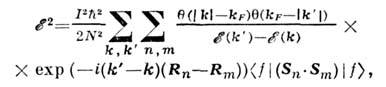

где N - число ионов,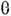- ступенчатая тета-функция Дирака,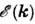- дисперсии закон электронов проводимости (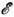- энергия,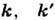- волновые векторы), kp - значение волнового вектора на Ферми-поверхности| 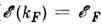- Ферми-энергия],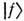- вектор состояния, описывающий основное состояние f -подсистемы. Эта поправка соответствует эфф. гамильтониану гейзенберговского типа (см. Гейзенбергамодель):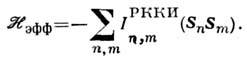

Число f -электронов и, следовательно, величина спина S_n одинаковы для всех ионов. Зависимость интеграла 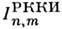от расстояния между магн. ионами 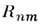= 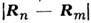определяетсязаконом дисперсии электронов проводимости 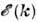и степенью заполненности проводимости зоны. Строгий расчёт 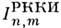осложнён учётом вклада от электронов, лежащих глубоко под поверхностьюФерми, где их нельзя считать квазисвободными при любом законе дисперсии. Эфф. гамильтониан можно определить, предположив квадратичный закон дисперсииэлектронов проводимости 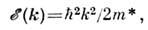где m* - эффективная массаs-электрона. Тогда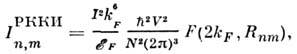

здесь V - объём тела, 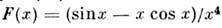(график этой ф-ции изображён на рис.). Ф-ция 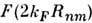определяет зависимость обменного интеграла 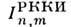от расстояния R_nm между магн. ионами. В зависимости отвеличины R_nm обмен может быть ферромагнитным (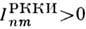, и антиферромагнитным 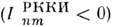. С ростом расстояния R_nm осцилляции затухают и при большихрасстояниях.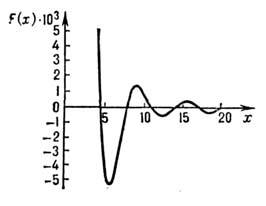

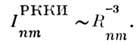
В отличие от короткодействующего прямого OВ. РККИ-о. в. имеет большойрадиус. Интеграл 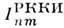сильно зависит от концентрации свободных носителей заряда n_s. Т. к. 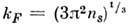,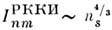.Поэтому в диэлектриках, где концентрация свободных носителей заряда оченьмала, РККИ-о. в. можно не учитывать. РККИ-о. в. позволяет объяснить существованиеразл. магн. структур. Так, если ближайшие магн. соседи расположены на расстояниях, при к-рых 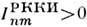,то осуществится ферромагн. упорядочение, если 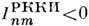,-то антиферромагнитное. Более сложные магн. структуры, напр. геликоидальные, можно также объяснить с помощью существования знакопеременного 0В.

Лит.:1)Ruderman M. А., К i t t e 1 С., Indirect exchangecoupling of nuclear magnetic moments by conduction electrons, «Phys. Rev.»,1954, v. 96, p. 99; 2) К a s u у а Т., A theory of metallic ferro- andantiferromagnetism on Zencr's model, «Progr. Theor. Phys.», 1956, v. 16,p. 45; 3) Y о s i d a K., Magnetic proper i. > of Cu-Mn alloys, «Phys.Rev.», 1957.,. v. 106, p. 893; 4) У а и т Р. М., Квантовая теория магнетизма, пер. с англ., 2 изд., М., 1985. А. В. Ведяев, О. А. Котелънипова.