Akademik

ПОЛЕ в квантовой механике - эффективное(в простейших случаях среднее по времени) силовое поле, создаваемое частицамисложной системы (атома, атомного ядра, твёрдого тела и др.). Служит дляприближённого описания взаимодействия между частицами путём его заменывоздействием С. п. на каждую из них; при этом решение многочастичной задачисводится к рассмотрению движения отд. частицы в С. п. (и во внеш. поле, если оно имеется). Имея сходную с последним структуру, С. п. отличаетсятем, что зависит от состояния системы, определяемого самим же С. п. Этотребует согласования вида С. п. с решениями динамич. ур-ний, зависящимив свою очередь от С. п., с чем и связан термин «самосогласованное».

С. п. описывает лишь часть взаимодействия между частицами, отвечающуювоздействию ср. распределения частиц системы на каждую из них. За рамкамиметода С. п. остаётся корреляционная (флуктуационная) часть взаимодействия, связанная с отличием мгновенного распределения частиц от среднего. Во мн. случаях корреляции играют незначит. роль и применение метода С. п. оправдано. Однако в ряде явлений (критич. явления, силы Ван-дер-Ваальса и др.) этароль является определяющей.

Понятие С. п. в первонач. форме возникло в небесной механике, а затемвошло в теорию мн. частиц при описании ферромагнетизма [теория молекулярногополя, П. Вейс (P. Weiss, 1907)], пространственного заряда [теория газовогоразряда, И. Ледгмюр (I. Langmuir, 1913)], тяжёлого атома [ Томаса-Фермиметод, Л. Томас (L. Thomas, 1927), Э. Ферми (Е. Fermi, 1928)]. Строгоеквантовомеханич. обоснование метода С. п. было дано Д. Хартри (D. Hartree,1928) и В. А. Фоком (1930) вскоре после создания квантовой механики.

Для формулировки метода С. п. и понимания его смысла существенна особаяроль взаимодействия в многочастичных системах. Порождая многообразие ихсвойств, взаимодействие сказывается и на способе теоретич. описания. Вотсутствие взаимодействия, когда движение частиц динамически независимо, объектом описания может быть отд. частица системы (одночастичная картина):состояние системы в целом полностью определяется состояниями каждой изеё частиц. Взаимодействие разрушает эту картину, лишая смысла понятие осостоянии отд. частицы. Можно говорить лишь о состоянии системы как целого, к-рая и становится теперь объектом описания. Это ведёт к качественномуусложнению теории мн. частиц: вместо волновой ф-ции 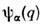отд. частицы (q - совокупность пространственной, спиновой и др. координат, 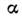-индекс состояния) вводят зависящую от N координат (N - числочастиц в системе) волновую ф-цию всей системы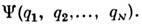

Идея метода С. п. состоит в том, чтобы сохранить одночастичную картинуипри наличии взаимодействия, частично компенсируя возникающие при этом ошибкивведением дополнит. (помимо внешнего) силового поля. Это поле, к-рое иназ. С. п., подбирают так, чтобы свести указанные ошибки к минимуму. Поэтомуметод С. п.- наилучший из всех возможных способов одночастичного описаниясистемы взаимодействующих частиц. При относит. простоте матем. аппарата(наиб. сложна процедура самосогласования) этот метод даёт эфф. описаниевзаимодействия между частицами, если эффекты корреляц. взаимодействия невелики.

Основные уравнения. Одночастичному характеру метода С. п. отвечаетмультипликативная структура волновой ф-ции системы:

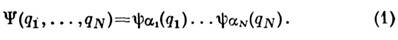
Для тождественных бозе-(ферми-)частиц нужна симметризация (антисимметризация)ф-ции (1) по координатам, обозначаемая символом S:

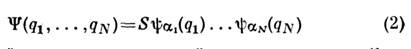
(в случае ферми-частиц это ведёт к детерминанту Слэ-тера - Фока). Вчастности, при N = 2:
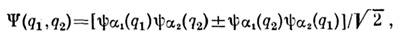где здесьи ниже знаки «+» и «-» отвечают бозе-(ферми-) частицам. Различию правыхчастей (1) и (2) отвечают обменные (статистич.) корреляции (см. Обменноевзаимодействие), присущие тождеств. частицам. В отличие от силовых(динамич.) корреляций, порождаемых взаимодействием и отвечающих его корреляц. части, обменные корреляции описываются методом С. п.

Матрица плотности системы в методе С. п. также сводится к произведениюодночастичных матриц плотности:

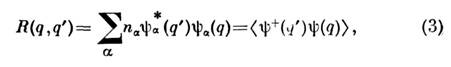
где п _а - числа заполнения уровней,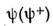- операторная ф-ция уничтожения (рождения) в методе вторичного квантования,«*»означает комплексное сопряжение, <...> - усреднение по состоянию системы. Так, парная матрица плотности имеет вид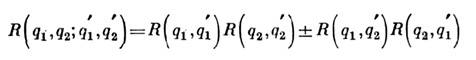

(в отсутствие обменных эффектов остаётся лишь первое слагаемое). Этовыражение (и соответствующую ф-лу для ф-цпй распределения) используют вприложениях метода С. п. к термодинамике и кинетике.

Одночастичную волновую ф-цию 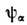выбирают в методе С. п. из условия макс. близости выражений (1), (2) кточной волновой ф-ции системы. С этой целью используют вариац. принцип. требующий минимума энергии системы 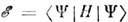при условии 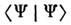= 1, где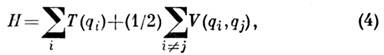

Н - гамильтониан системы, Т - сумма кинетич. энергии ивнеш. поля, V - взаимодействие между частицами, i, j =1,2, ..., N. Волновая ф-ция (1) приводит к ур-нию Хартри для

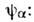
включающему С. п.

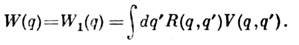
Волновая ф-цпя (2) приводит к ур-нию Хартри- Фока, имеющему вид (5)с 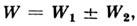гдеобменный член W₂ определяется соотношением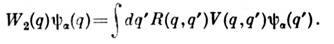

Через одночастичные энергии 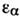выражается полная энергия системы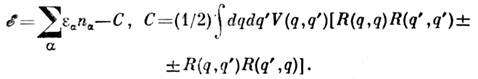

Согласно варпац. принципу эта величина всегда больше истинного значенияэнергии.

Величина W₁ имеет простой смысл ср. поля частиц системы, действующего на данную частицу, a W₂ ведёт к увеличению(уменьшению) вероятности сближения двух бозе-(ферми-)частиц, изменяя соответств. образом их взаимодействие. Самосогласованному характеру величины W отвечаетзависимость матрицы плотности (3) от решений ур-ния (5), к-рое становитсянелинейным и может поэтому иметь более одного набора решений. Так, привыполнении нек-рых условий возможно сосуществование двух решений ур-ния(5), отвечающих однородному и неоднородному состояниям системы, каждоеиз к-рых устойчиво в своей области плотностей и темп-р. Это соответствуетфазовому переходу со спонтанным нарушением трансляц. симметрии и с появлением волнзарядовой плотности.

В др. формулировке метода С. п. заменяют гамильтониан (4) выражением, к-рое соответствует одночастичной картине. В методе вторичного квантования, где

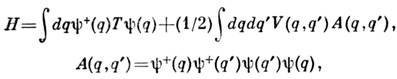
эту картину нарушает входящий во взаимодействие оператор А, содержащийчетыре операторные ф-ции вместо нужных двух. Модифициров. гамильтониан, отвечающий методу С. п., соответствует замене в А комбинаций 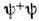их ср. значениями (матрицами плотности):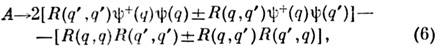

и имеет вид

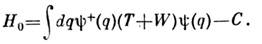
Это выражение приводит к ур-нию Хартри - Фока (5) и в то же время реализуетминимум величины 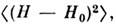что и соответствует методу С. п. как наилучшему из одночастпчных способовописания. Применения метода. Простейший объект приложения метода С. п.-бесконечная однородная система взаимодействующих по закону Кулона ферми-частицс массой т, зарядом е и спином ¹/₂ (электронов)в присутствии однородного компенсирующего фона противоположного знака заряда. В методе С. п. энергия такой системы в единице объёма равна 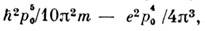где 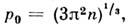п- плотность числа частиц, первый член - кинетическая, второй - обменнаяэнергия. Этот результат используют для упрощения интегродифференц. ур-нияХартрп - Фока (5), заменяя его дифференц. ур-нием Хартри - Фока - С л этер а, где 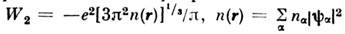-локальное значение плотности числа частиц.

Др. упрощённым вариантом метода С. п. является метод Томаса - Ферми(квазиклассич. приближение к методу С. п.), применимый к слабо неоднороднымсистемам, где ср. расстояние между частицами меньше характерной длины, на к-рой заметно меняется плотность п др. параметры системы. В методе Томаса- Ферми используют выражения, справедливые для однородной системы, относяих в каждой точке к соответств. локальному значению плотности. Этот методиспользуют для описания тяжёлых атомов, вещества в экстремальных условияхвысоких давлений или темп-р и др. Применяют и иные, более частные способыупрощения метода С. п. (напр., в теории атома часто используют усреднениеС. п. по углам, упрощающее отделение угл. переменных).

Метод С. п. находит применение в физике атома и молекулы, ядерной физике, физике конденсиров. состояния вещества, физике плазмы и др. областях науки. Часто он даёт достаточно точное описание системы мн. частиц. Это относится, в частности, к атомно-молекулярной физике и теоретич. спектроскопии, гдеметод С. п. применяют особенно широко благодаря относительно малому вкладукорреляц. эффектов. Напр., в атоме Не (простейшей системе мн. частиц) этотвклад составляет ~ 1,5% от полной энергии электронной оболочки.

К числу др. важных применений метода С. п. в теории систем мн. частицотносятся описание равновесных п кинетич. свойств плазмы в бесстолкновит. режиме, Ландау теория фазовых переходов 2-го рода и др.

Обобщения метода. Существует ряд обобщений метода С. п., приспособленныхдля частичного описания корреляц. эффектов. Так, при необходимости учётапарных корреляций сверхпроводящего типа используют модифициров. гамильтониан(6), где заменяют ср. значениями комбинации 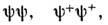что приводит к ур-ниям Хартри - шока - Боголюбова. Такой подход применяютв теории сверхпроводимости и в теории атомного ядра. Для описания многочастичных(дальних) корреляций, отвечающих поляризац. эффектам в кулоновской системе, используют зависящее от времени ур-ние Хартри - Фока: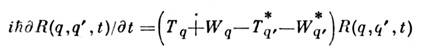

(индекс указывает переменную, на к-рую действует оператор). Это ур-ниеопределяет нестационарную одночастичную матрицу плотности и оказываетсяравноценным приближению случайных фаз (приближению высокой плотности),совпадая в то же время с кинетич. ур-нием, включающим С. п. без учёта столкновений. Его применяют для описания коллективных возбуждённых состояний системы.

При необходимости систематич. описания корреляц. эффектов метод С. п. служит хорошим исходным приближением для последующего применения теориивозмущения и диаграммной техники. Корреляц. части взаимодействия отвечаетгамильтониан H'= H - H₀. Выбор при описании системы взаимодействующихчастиц картины С. п. (а не картины невзаимодействующих частиц) в качествеисходного приближения упрощает ма-тем. аппарат описания корреляц. эффектов, в частности сокращается число диаграмм теории возмущений.

В последние годы в теории мн. частиц получил широкое распространениеполуфеноменологпч. метод функционала плотности, обобщающий подход, основанныйна ур-ниях Хартри - Фока - Слэтера и предназначенный для описания не толькообменных, но и силовых корреляций. В этом методе используют ур-ния Кона-Шэма, имеющие вид ур-ний (5) с где член W₂, описывающий корреляцииобоих типов, выбирают в виде относительно простого функционала плотности. Имея ограниченную и не всегда ясную область применимости, методфункционала плотности тем не менее успешно используется в физикеатома, атомного ядра и в физике конденсиров. сред (в частности, для расчётовзонной структуры твёрдых тел, для описания поверхностных явлений). Лит.: ФокВ. А., Многоэлектронная задача квантовой механики и строение атома, в кн.:Юбилейный сборник АН СССР, ч. 1, М- Л. 1947, с. 255; Хартри Д. Р., Расчетыатомных структур, пер. с англ., М., 1960; Т а у л е с Д., Квантовая механикасистем многих частиц, пер. с англ., 2 изд., М., 1975, К и р ж н и ц Д. А., Полевые методы теории многих частиц, М 1963; Слэтер Дж., Методы самосогласованногополя для молекул и твердых тел, пер. с англ., М., 1978; Теория неоднородногоэлектронного газа, пер. с англ., М., 1987. Д. А. Киржниц.