Akademik

дифференциально-геометрическая - правило, сопоставляющеекаждому тензору 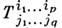типа ( р, q )его ковариантную производную 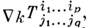являющуюся тензором типа ( р, q + 1). В координатах х ¹,...,х ^п С. задаётся набором Кристоффе-ля символов 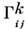по ф-ле: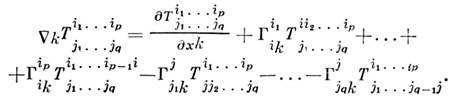

При замене координат 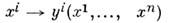величины 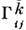должны заменяться на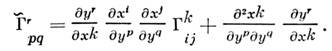

С. определяет параллельный перенос тензоров вдоль кривых: тензор . параллелен вдоль кривой 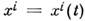, i = l,..., п, если 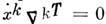. Ур-ниями определены геодезич. С.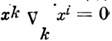

Тензор кручения С. определяется ф-лой 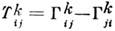С. с нулевым кручением наз. симметричной. Кривизна С. определяется кривизнытензором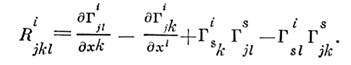

Через кривизну и кручение выражаются коммутаторы ковариантныхпроизводных, напр. для векторов Т ⁱ имеем:

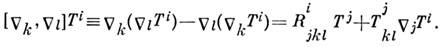
Евклидова С. задаётся, по определению, условиями в нек-рых координатах;в этом случав координаты 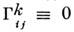наз. евклидовыми. В таких координатах ковариантные производные совпадаютс частными. Тем самым евклидова С. определяет правила дифференцированиятензоров в любых криволинейных координатах. С. является евклидовой(локально), если её кривизна и кручение равны нулю.

В римановом пространстве (или псевдоримановом пространстве) С, однозначно определяется по римановой метрике ( индефинитной метрике)g_ij условиями 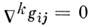, 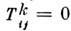. Параллельныйперенос при этом сохраняет длины векторов и углы между ними: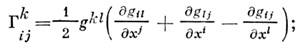

тензор кривизны этой С. наз. тензором кривизны риманова пространства.

С. и построенные по ней тензоры используются в ур-ниях общей теорииотносительности.

С. в расслоении со структурной группой G - то же, что калибровочное поле. Поля 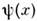, принимающие значения в зарядовом пространстве, играют при этом роль тензорныхполей. Если А _i (х)- калибровочное поле, принимающее значениев Ли алгебре L(G) группы G симметрии зарядового пространства (т. е. матричнозначное), то ковариантные производные поля 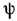определяются ф-лами: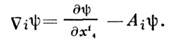

Осн. их свойство - при локальных зарядовых преобразованиях 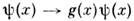[где ф-ция g(x )принимает значения в группе GJ и калибровочныхпреобразованиях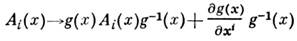

производная 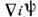преобразуется ковариантно: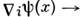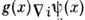. Это даёт однозначный рецепт введения взаимодействия полей A_i(x )и 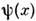: если 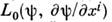-свободный лагранжиан поля 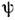,инвариантный относительно зарядовых преобразований, то лагранжиан 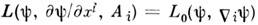описывает калибровочно-инвариантное взаимодействие полей А _i и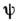

Параллельный перенос поля 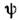вдоль кривой xⁱ = xⁱ(t )определяется из ур-ния 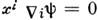.Кривизна С. в расслоении определяется ф-лой: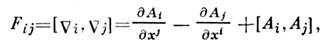

где скобки обозначают коммутатор. При калибровочных преобразованияхона меняется по закону:

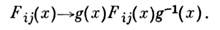
Если кривизна С. равна нулю, то калибровочное поле локально представляетсяв виде

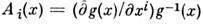
и калибровочным преобразованием приводится к нулевому. Кривизна С. определяетизменение поля 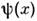при параллельном переносе вдоль контура бесконечно малого параллелограммасо сторонами 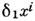,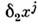: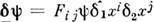. Она удовлетворяет тождеству Б ь я н к и: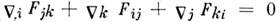,где 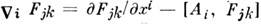. В полный лагранжиан калиоровочных теории, используемых, напр., в теории сильных взаимодействий, кривизна входит в инвариантной комбинации- 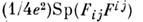(здесьSp - след матрицы, е - заряд).

Лит.: Славнов А. А., Фаддеев Л. Д., Введение в квантовую теориюкалибровочных полей, 2 изд., М., 1988; Дубровин Б. А., Новиков С. П., ФоменкоА. Т., Современная геометрия, 2 изд., М., 1986. Б. А. Дубровин.