Akademik

- отображение, сопоставляющее каждой паре е ₁,е ₂ векторов к.-л. векторного пространства L нек-роечисло (e₁, е ₂), причём выполняются след. условия:а) 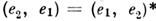(*означает комплексное сопряжение); б)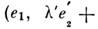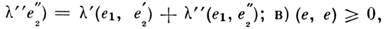(e,e) = 0 лишь при е =0. Из этих аксиом следуют неравенство Коши- Буняковского - Шварца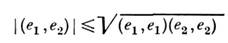

и антилинейность С. п. по первому аргументу, т. е.

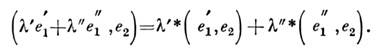
С. п. порождает в L н о р м у, т. е. операцию, сопоставляющуюкаждому вектору е вещественное неотрицательное число 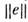,к-рое служит обобщением понятия длины вектора е,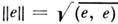. Т. о., пространство L оказывается нормированным. Норма задаёттопологию пространства L, т. е. определяет в нём понятие близости: последовательность е ₁,е ₂, ..., е _п, ... векторов считается сходящейсяк вектору «, есл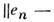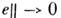и -при 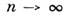.Пространство L наз. полным, если любая последовательность векторов е ₁,..., е _п... (такая, что 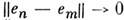при га, )имеет предел е, являющийся вектором того же L. Если (e₁,e₂)= 0, то векторы e₁ и е ₂ наз. ортогональными. Если 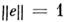, то вектор наз. нормированным. Совокупность e₁, е ₂,...,е _п наз. ортонормированной системой векторов, еслиона состоит из нормированных, попарно ортогональных векторов.

Конечномерное пространство L, снабжённое С. п., наз. евклидовымпространством. Если L является бесконечномерным и полным, тооно наз. гильбертовым пространством. С. п. ( е ₁, е), гдевектор e₁ фиксирован, а вектор е рассматриваетсякак переменная, определяет числовую ф-цию f(e) - (e₁, е )нагильбертовом пространстве. Эта ф-ция линейно зависит от е иобладаетсвойством непрерывности [если 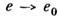, то 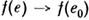],её называют линейным функционалом.

В гильбертовом пространстве всякий линейный функционал i(e )порождаетсяС. п., т. е. всегда найдётся такой вектор e₁, что f(e)= (e₁, е).

Лит.: Дирак П. А. М., Принципы квантовой механики, пер. с англ.,2 изд., М., 1979; Кострикин А. П., М а н и н Ю. И., Линейная алгебра игеометрия, 2 изд., М., 1986. О. И. Завьялов.