Akademik

- случайная ф-ция 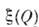носк. непрерывных переменных (параметров)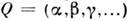,т. е. такая ф-ция, реализации к-рой подчиняются вероятностным законам, задающим значение ф-ции в каждой точке пространства и взаимосвязь значенийв соседних точках. Число независимых переменных фиксирует размерность пространства, на к-ром задано С. п. Если одним из параметров является время t,то говорят о переменном С. п. в пространстве, размерность к-рого определяетсячислом остальных параметров. Напр.,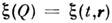- переменное С. п. в трёхмерном пространстве ( х, у, z), наз. такжепространственно-временным С. п. Такие С. п. чаще всего встречаются в физике.

С. п. используют при вероятностном описании флуктуац. явлений в системахс распределенными параметрами, в частности при описании флуктуацииплотности, темп-ры, диэлектрич. проницаемости и др. параметров разл. сред, при исследовании флуктуации эл.-магн. и звуковых волн, распространяющихсяв случайно-неоднородных средах, в задачах пространственно-временного приёмаи обработки сигналов на фоне шумов и помех, при описании полей шумов ипомех разл. происхождения, при вероятностной трактовке нек-рых результатовквантовой теории и т. д.

С. п., описываемое N ф-циями 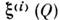, i= 1, 2, ..., N, наз. N-мерным. Компоненты 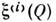в общей случае имеют разл. физ. природу (напр., совокупность давления, плотности и трёх компонент скорости), особый интерес представляет случай, когда величины 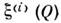имеют одинаковую размерность и преобразуются как компоненты вектора (тензора)при преобразованиях системы координат. В этом случае говорят о векторном(тензорном) С. п.

Основные понятия. Для С. п. используют те же способы заданияи статистич. описания, что и для случайных процессов, нужно тольковместо одной переменной t всюду подразумевать совокупность параметров Q. В частности, на С. п. обобщаются n-точечная плотность вероятности

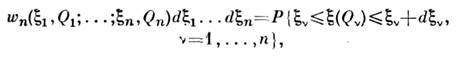
к-рая должна удовлетворять условиям неотрицательности, согласованностии нормировки, а также связанная с ней преобразованием Фурье n-мерная характеристическаяфункция

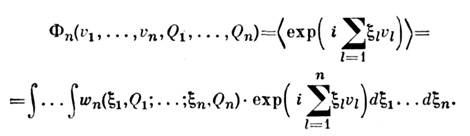
В теории С. п. используют функциональные методы, при этом вводят функционалплотности вероятности, являющийся континуальным обобщением w_n, либо характеристич. функционал

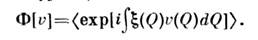
Моментные ( М )и кумулянтные ( К )ф-ции выражаются черезхарактеристич. функционал при помощи функциональных (вариационных) производных:

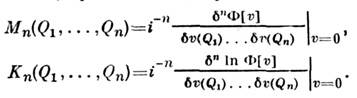
При статистич. описании С. п. необходимо учитывать причинно-следственныесвязи поля на оси времени и его возможные специфич. свойства, такие, какоднородность и изотропность, на разл. гиперповерхностях n-пространства.

С. п. наз. статистически однородным в узком смысле, если все его статистич. характеристики не изменяются при преобразовании трансляции 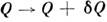. Если указанным свойством обладают только ср. значение и корреляц. ф-ция, то говорят о статистич. однородности в широком смысле. Многомерные С. п.,обладающие таким свойством, наз. однородными и однородно связанными.

Понятие статистич. однородности С. п. является обобщением понятия стационарностислучайного процесса. Если речь идёт о пространственно-временных С. п.,то различают стационарность поля по времени и его однородность по пространств. координатам, при этом С. п. может быть статистически однородным по частикоординат и неоднородным - по остальным. Иногда С. п. однородны толькона нек-рых поверхностях (на плоскости, на сфере и т. п.). Статистич. однородностьможет иметь место но пространственно-временному аргументу, напр. по аргументуr - vt в случае т. н. «замороженных» неоднородностей, движущихсякак целое равномерно со скоростью v и описываемых С. п.

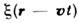
При статистич. описании С. п. часто ограничиваются корреляционнойтеорией, в к-рой используют только моменты 1-го и 2-го порядка, т. е. ср. значение

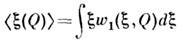
и корреляц. ф-цию

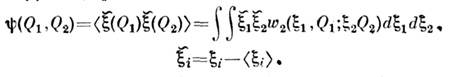
Характерный масштаб убывания корреляц. ф-ции наз. масштабом или радиусомкорреляции. Напр., С. п. с гауссовой корреляц. ф-цией

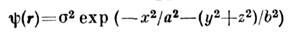
имеет масштаб корреляции а вдоль оси х и радиус корреляции b в плоскости (y,z). Корреляц. теория точно описывает толькополя с нормальным (гауссовым) законом распределения вероятностей.

Многомерное С. п.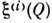в рамках корреляц. теории характеризуется совокупностью ср. значений 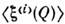и корреляц. матрицей 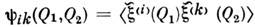,в к-рой диагональные элементы представляют собой ф-ции автокорреляции, а недиагональные - ф-ции взаимной корреляции компонент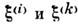

В приложениях приходится иметь дело с комплексными С. п.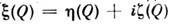, полное статистич. описание к-рых не отличается от описания двумерногоС. п. с компонентами 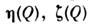.Обычно не производят разделения С. п. на вещественную и мнимую части, аоперируют непосредственно с 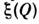и комплексно сопряжённым полем 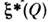.При описании таких С. п. в рамках корреляц. теории приходится поэтому рассматриватьдве корреляц. ф-ции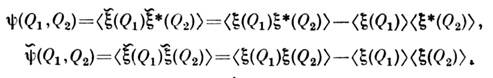

через к-рые выражаются ф-ции корреляции вещественной и мнимой частейкомплексного С. п.:

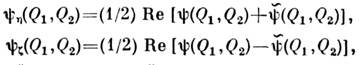
а также ф-ции взаимной корреляции

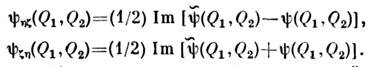
Для случайного эл.-магн. поля с напряжённостью электрич. поля Е(r )вводят поляризационную матрицу 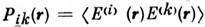. С её помощью вычисляются Стокса параметры, характеризующие состояниеполяризации С. п.

Простейшей мерой статистич. связи значений С. п. в разных точках Q-пространстваявляются коэффициенты корреляции:

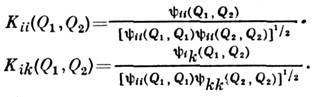
Пространственно-однородные поля, у к-рых 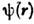и 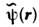зависят толькоот модуля вектора r = r₁ - r₂, т. е.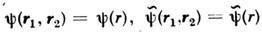,наз. статистически изотропными в широком смысле. (Изотропность в узкомсмысле подразумевает аналогичные свойства непосредственно у плотностейвероятности.) Многомерные С. п., у к-рых указанным свойством обладают ф-циикорреляции, являются изотропными и изотропно связанными. Как и однородность, изотропность полей может иметь место лишь на нек-рых гиперповерхностяхпространства независимых переменных.

Для статистически однородных (в широком смысле) С. п. справедливо обобщение Винера - Хинчина теоремы, устанавливающее взаимосвязь между корреляц. ф-цией и пространственно-временной спектральной плотностью G(w,k). Дляполя, стациенарного по времени и однородного в трёхмерном пространстве, эта связь имеет вид:

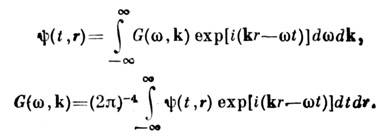
Через пространственно-временную спектральную плотность G(w,k) выражаются пространственный Ф(k) и временной (частотный) g(w )спектрыС. п.:

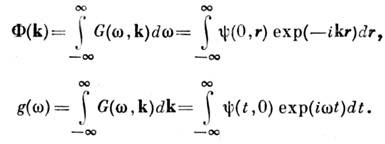
Для многомерных однородных и однородно связанных С. п. аналогичная связьимеется между элементами корреляц. матрицы 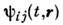и соответствующими элементами матрицы спектральной плотности 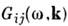Ввиду положит. определённости матрицы 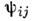диагональные элементы матрицы 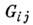вещественны и неотрицательны, а недиагональные элементы могут быть комплексными.

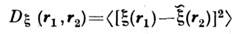Пространственным аналогом случайного процесса со стационарными приращениямиявляется локально одноподное С. п., для к-рого разность ср. значений и структурная ф-ция зависят только от разности r = r₁ - r₂. Еслиэти величины зависят только от модуля г, говорят о локально изотропномС. п. Локально однородные и локально изотропные С. п. используют, напр.,при описании флуктуации параметров турбулентных сред.

В рамках корреляц. теории локально однородные С. п. можно также описыватьпри помощи спектральной плотности Ф(k). Из-за расходимости интеграла при 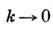корреляц. ф-ции для таких С.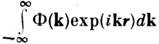п. не существуют, а структурная ф-ция существует, т. к. интеграл сходитсяпри

менее жёстких 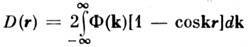требованиях. Это следствие «нечувствительности» структурной ф-ции к флуктуациям, пространственные масштабы к-рых превышают рассматриваемое расстояние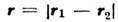

Аналогом квазистационарных процессов являются квазиоднородные С. п.,у к-рых многоточечные статистич. характеристики слабо зависят от координатцентра тяжести рассматриваемых точек r₁, r₂,...,r_n по сравнению с зависимостью от взаимного расположения этих точек, т. е. от разностей r_j - r_k. Для таких С. п. вводят понятие локальной спектральной плотности, равной преобразованиюФурье пространственной корреляц. ф-ции по разностным переменным r =r₁ - r₂.

Марковские случайные поля. В физ. задачах часто рассматриваютС. п., заданные при помощи стохастических уравнений, т. е. динамич. ур-ний, содержащих случайные сторонние воздействия. Вид динамич. ур-ннйопределяется физ. закономерностями, а в качестве сторонних воздействий, описывающих источники случайных возмущений, часто используют С. п., дельта-коррелированныепо тем или иным переменным. Исследуемое С. п. при этом является марковскимпо указанным переменным, что упрощает вычисление его статистич. характеристик.

Важным примером таких С. п. являются поля равновесных тепловых флуктуациив электродинамике, описываемые Максвелла уравнениями с дельта-коррелированнымисторонними токами j_e(r )и i_m(r):

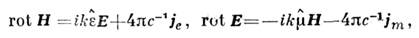
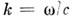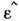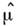где - волновое число,и -комплексные тензоры диэлектрич. и магн. проницаемостей среды с компонентами ,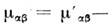-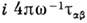. Элементыкорреляц. матрицы векторных полей j_e и j _т зависят от электрич. и магн. проводимостей среды 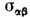и 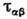и в соответствиис флуктуационно-диссипативной теоремой описываются выражениями: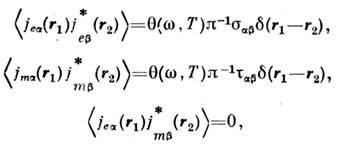

где 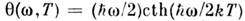- ср. энергия квантового осциллятора с собств. частотой w при абс. темп-ре Т. к-рая в классич. области 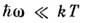переходитв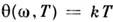

К С. п. такого типа приводит также т. н. марковского процесса приближение в теории распространения волн в случайно-неоднородных средах. В этомприближении волновое поле описывается параболич. ур-нием, в к-ром флуктуац. часть диэлектрич. проницаемости среды полагают дельта-коррелированной внаправлении распространения падающей волны (см. Параболического уравненияприближение).

Понятие марковского С. п. тесно связано с причинностью, под к-рой понимаютфункциональную зависимость С. п. в данной пространственно-временной точкеот предшествующих значений поля по временной или пространственной координате. В общем случае не всегда удаётся выделить в пространстве координату илисовокупность координат, по к-рым исследуемое С. п. можно было бы считатьмарковским. Эта трудность не возникает, если речь идёт о марковских С. п. по времени. Такие С. п. используют в неравновесной термодинамике, встатистич. гидромеханике, а также в теории оптимальной пространственно-временнойобработки случайных сигналов на фоне шумов и помех. Примером С. п. такоготипа является поле 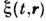, удовлетворяющее стохастич. ур-нию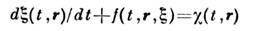

с аддитивным сторонним воздействием 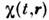, обладающим корреляц. ф-цией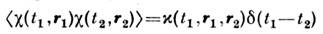

Если распределение 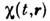гауссово, то для функционала плотности вероятности этого С. п. справедливообобщённое Фоккера - Планка уравнение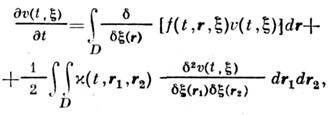

в к-ром вместо частных производных фигурируют функциональные производныеи, кроме того, интегрирование по r проводится в пределах той области пространства D, на к-рой задано С. п.

При нач. условии 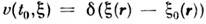это ур-ние описывает функционал плотности вероятности перехода С. п. изначального (в момент t₀) состояния 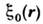в состояние 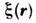втекущий момент t. Описанное ур-ние (как и вообще подобные ур-ниядля функционалов плотности вероятности) имеет символич. смысл, поcколькунормировочные константы величин 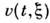обычно обращаются в 0 или в 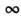.С матем. точки зрения более корректно было бы оперировать с характеристич. функционалами, свободными от этого недостатка. Однако в физ. приложенияхпредставляют интерес такие статистич. характеристики С. п., к-рые не зависятот нормировочных констант: моментные и кумулянтные ф-ции, отношение функционаловплотности вероятности (т. н. отношение правдоподобия) и др. Для вычисленияэтих величин можно использовать обобщённое ур-ние Фоккера - Планка. К болеесложным ур-ниям для функционала плотности вероятности полей приводит учётнегауссовых сторонних воздействий (при сохранении их дельта-коррелированностипо времени), неаддитивность этих воздействий в стохастич. ур-ниях и многомерностьрассматриваемого С. п.

Лит.: М о н и н А. С., Я г л о м А. М., Статистическая гидромеханика, ч. 1-2, М., 1965-67; Хохлов Р. В., Маков Ю. Н., О марковских волновых процессах, в сб.: Проблемы математической физики и вычислительной математики, М.,1977; Введение в статистическую радиофизику, ч. 2 - Рытов С. М., КравцовЮ. А., Т а т а р с к и й В. И., Случайные поля, М., 1978; Кляцкин В. И.,Стохастические уравнения и волны в случайно-неоднородных средах, М., 1980;Розанов Ю. А., Марковские случайные поля, М., 1981; Ахманов С. А., ДьяковЮ. Е., Чиркин А. С., Введение в статистическую радиофизику и оптику, М.,1981. Ю. А. Кравцов, А. Б. Шмелёв.