Akademik

- равновесное макроскопич. состояние термодинамической системы, к-рое фиксируется заданием параметров состояния, представляющих собой измеряемые макроскопич. приборами ср. величины определ. набора характеристик системы. Конкретный выбор этих параметров неоднозначен и определяется тем, каким способом рассматриваемая равновесная система выделяется из среды окружающих её тел и др, систем (т. е. видом контакта системы и окружения). Обычно используется один из четырёх вариантов такого выбора: 1) адиабатически изолированная система (система выделена стенками, не допускающими через себя потоки энергии и частиц) - фиксируются энергия системы 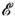, объём V, число частиц N и внеш. поля X;2) система в термостате (система выделена с помощью теплопроводящих стенок и находится в равновесии с др. термодинамич. системой, выполняющей роль термометра или термостата) - фиксируются темп-pa Т или Q= kT (энергия 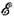уже не фиксируется точно), а также V, N, X;3) система выделена воображаемыми стенками (величины 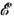и N точно не фиксированы)- в качестве параметров состояния используются Q, V, X и хим. потенциал m; 4) вариант 2, но с подвижной стенкой (система "под поршнем", выполняющим роль мембраны манометра, объём V уже точно не фиксирован) - параметрами состояния являются Q, давление P, N и X. В термодинамич. пределе, 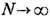, V/N=const, все четыре варианта оказываются эквивалентными, т. к. различия в граничных условиях проявляются как негарантированные малые поправки.

При выборе параметров в варианте 1 потенциалом термодинамическим, содержащим в себе всю информацию о равновесных свойствах системы, является энтропия S = S(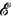, V, N, X), в варианте 2-свободная энергия ( Гелъмгольца энергия) F=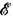-QS/k = F(Q,V,N,X), в варианте 3 - введённый Гиббсом потенциал W = F- mN== W (Q, V, X, m) и в варианте 4 - Шббса энергия (потенциал Гиббса) G = F+PV=G(Q, P, X,N). Если зафиксировать условие 1, то энтропия при стремлении системы к равновесному состоянию достигает своего макс. значения, при фиксир. условиях 2, 3, 4 соответственно потенциалы F,W, G стремятся к своим мин. значениям. Т. о., единственное и устойчивое состояние равновесия термодинамического, характеризуемое не только внеш. условиями, но и значениями всех др. макроскопич. параметров, определяется как решение вариационной задачи, соответствующей выбору одного из вариантов 1 -4 в случае 1 - 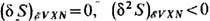, в случае 2 - (dF)_QVXN =0,(d²F)_QVXN > 0 и т. д. Вариации термодинамич. потенциалов производятся по тем параметрам системы, к-рые при указанных фиксир. условиях могут принимать неравновесные значения.

Состояния неравновесных статистич. систем фиксируются по-разному в зависимости от этапов их эволюции. Напр., для классич. неидеального газа в нач. период времени, меньший или порядка времени взаимодействия отдельных частиц друг с другом, микроскопич. состояние системы определяется как в механике - заданием импульсов и координат всех N частиц. Затем состояние хаотизируется, индивидуальность частиц утрачивается и система вступает в кинетич. фазу эволюции, описываемую кинетич. ф-циями распределения и кинетич. ур-ниями (см. Кинетическая теория газов). По истечении времени t~т _пр (т _пр - ср. время свободного пробега) в областях системы, имеющих локальный размер ~l (l -ср. длина свободного пробега), возникает локальное термодинамическое равновесие. Темп-ра Q (t, r), плотность n(t, r )и др. определяемые ими термодинамич. характеристики являются локальными и зависят от времени t и пространственной координаты r. На этом этапе эволюция системы описывается ур-ниями гидроди-намич. типа с учётом неоднородностей темп-ры, плотности и конкретных граничных условий ( Навье -Стокса уравнения, ур-ния теплопроводности, диффузии и др.), а состояние- как "карта" релаксирующих значений локальных термодинамич. характеристик. Лишь по истечении общего времени релаксации в системе прекращаются потоки, устанавливаются равновесные значения темп-ры (одинаковые для всех r), плотности, давления и т. д. (при наличии внеш. статич. поля эти величины неоднородны и зависят от r), утрачивается роль граничных условий, кинетических коэффициентов и т. д. При этом поведение системы описывается методами равновесной термодинамики, состояние фиксируется условиями 1-4, а сама система конкретизируется с помощью макроскопич. ур-ний состояния или соответствующим термодинамич. потенциалом.

Лит.: Квасников И. А., Термодинамика и статистическая физика. Теория неравновесных систем, М., 1987; его же, Термодинамика и статистическая физика. Теория равновесных систем, М., 1991. И. А. Квасников.